Capitolo 11 - La Circolazione Oceanica Forzata dal Vento

Che cosa forza le correnti oceaniche? Sulle prime, possiamo rispondere, che il vento guida la circolazione. Ma se pensiamo con più attenzione alla domanda, possiamo non essese sicuri di ciò. Per esempio, possiamo notare che la controcorrente equatoriale nord nell'Atlantico e nell'oceano Pacifico vanno controvento. I navigatori spagnoli nel 16-mo secolo lungo le coste della Florida, notavano una forte corrente diretta a nord che sembrava non essere in relazione con il vento. Come si spiegava tutto questo? E, perché si trovavano delle forti correnti al largo delle coste orientali e non al largo di quelle occidentali?

Le risposte alle domande possono essere trovate in una serie di tre lavori fondamentali pubblicati dal 1947 al 1951. Nel primo, Harald Sverdrup (1947) mostrava che la circolazione nel primo kilometro dell'oceano é direttamente collegata al rotore dello sforzo del vento (wind stress). Henry Stommel (1948) mostrò che la circolazione di un 'gyre' oceanico é asimmetrica perché la forza di Coriolis varia con la latitudine. Infine, Walter Munk (1950) aggiunse la viscosità vorticosa (eddy viscosity) e calcolò la circolazione degli strati superficiali del Pacifico. Insieme, i tre oceanografi hanno gettato le basi della moderna teoria della circolazione oceanica.

11.1 La Teoria di Sverdrup sulla Circolazione Oceanica

Mentre Sverdrup stava analizzando le osservazioni delle correnti equatoriali, ?? he came upon (11.7) below relating the curl of the wind stress to mass transport within the upper ocean. ?? Nel derivare le relazioni, Sverdrup assunse che il flusso é stazionario, che l'attrito laterale e la viscosità molecolare sono piccole e che la turbolenza vicino alla superficie marina può essere descritta usando una viscosità vorticosa. Assunse anche che il flusso é baroclino e che la circolazione forzata dal vento scompare ad una certa profondità di 'no-motion'. Da (8.9 e 8.12) le componenti orizzontali dell'equazione del momento sono:

	(11.1a)
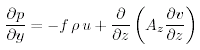	(11.1b)

Sverdrup integra queste equazioni dalla superficie ad una profondità -D eguale a o più grande della profondità a cui il gradiente di pressione orizzontale diventa zero. Egli definì:

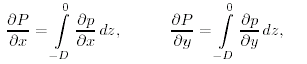	(11.2a)
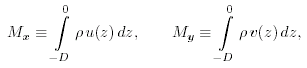	(11.2b)

dove M_x, M_y sono i trasporti di massa nello strato forzato dal vento che si estende fino alla profondità di 'no motion'.

La condizione al contorno alla superficie del mare é lo sforzo del vento e quella alla profondità -D é zero sforzo perché la corrente va a zero:

	(11.3)

dove T_x e T_y sono le componenti dello sforzo del vento.

Usando queste definizioni e le condizioni al contorno, la (11.1) diventa:

	(11.4a)
	(11.4b)

In modo simile, Sverdrup integrò l'equazione di continuità (7.19) sulla stessa profondità verticale, assumendo la velocità verticale alla superficie ed alla profondità -D sia zero, per ottenere:

(11.5)

Differenziando la (11.4a) rispetto a y e la (11.4b) rispetto a x, sottraendo, ed usando la (11.5) dà:

	(11.6)

dove β = ∂ f / ∂y é la derivata del parametro di Coriolis rispetto alla latitude, e dove curl_z(T) é la componente verticale del rotore dello sforzo del vento.

Questo é un risultato importante e fondamentale; il trasporto di massa verso nord delle correnti forzate dal vento é uguale al rotore dello sforzo del vento. Da notare che Sverdrup poneva f variabile con la latitudine. Vedremo in seguito che questo é essenziale.

calcoliamo β da

(11.7)

dove R é il raggio terrestre e φ é la latitudine.

Su gran parte dell'oceano,specialmente sui tropici, il vento é zonale e ∂T_y/∂x é sufficientemente piccolo che

(11.8)

Sostituendo la (11.8) nella (11.5) , Sverdrup ottenne:

(11.9)

Sverdrup integrò questa equazione dal bordo orientale nord-sud a x = 0, assumendo nessun flusso attraverso il bordo. Questo richiede M_x = 0 ad x = 0. Allora

(11.10)

dove Δx é la distanza dal bordo orientale del bacino oceanico, e le parentesi indicano una media zonale dello sforzo del vento (Figura 11.1).

Figura 11.1 Linee di flusso del trasporto di massa del Pacifico orientale calcolate dalla teoria di Sverdrup usando uno sforzo del vento medio annuale. Da Reid (1948).

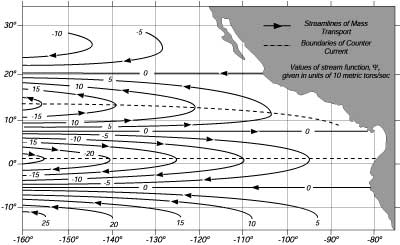
Per controllare la sua teoria, Sverdrup comparò i trasporti calcolati dai venti conosciuti nel Pacifico orientale tropicale con i trasporti dai dati idrologici raccolti da Carnegie e Bushnell nell'Ottobre e Novembre 1928, 1929, e 1939 tra 22°N e 10°S lungo 80°W, 87°W, 108°W, e 109°W. I dati idrologici furono usati per calcolare P integrando da una profondità di D = -1000m. Il confronto, Figura 11.2, mostra non soltanto che i trasporti possono essere accuratamente calcolati dal vento, ma anche che la teoria predice le correnti che vanno sopravento.

Figura 11.2 Trasporto di massa del Pacifico orientale calcolato dalla teoria di Sverdrup usando i venti osservati con la 11.9 e 11.11 (linee solide) e la pressione calcolata con i dati idrologici delle navi 11.4 (punti). Il trasporto é in tonnellate al secondo in una sezione larga un metro che si estende dalla superficie marina alla profondità di un kilometro. Notare la differenza tra le scale My e Mx. Da Reid (1948).

Commenti sulla Soluzione di Sverdrup

1. Sverdrup assume: i) Il flusso interno all'Oceano é geostrofico; ii) c'é una profondità uniform di 'no motion'; e iii) il trasporto di Ekman é corretto. Abbiamo visto la teoria di Ekman nel Capitolo 9, ed il bilancio geostroficofico nel Capitolo 10. Sappiamo poco della profondità di 'no motion' nel Pacifico tropicale.
2. Le soluzioni sono limitate al lato orientale degli oceani perché M_x cresce con x. The result stems from neglecting friction which would eventually balance the wind-driven flow. Tuttavia, le soluzioni di Sverdrup sono state usate per descrivere il sistema globale delle correnti di superficie. Le soluzioni sono applicate su ogni bacino sempre sul bordo occidentale del bacino. Lì, la conservazione della massa é forzata dall'includere le correnti nord-sud confinate ad un sottile, orizzontale strato sul bordo (Figura 11.3).

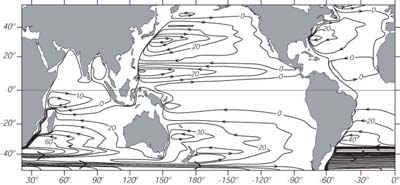
   Figura 11.3 Trasporto di Sverdrup integrato sulla profondità applicato globalmente usando lo sforzo del vento da Hellerman e Rosenstein (1983). L'intervallo dei livelli é di 10 Sv. Da Tomczak and Godfrey (1994).

3. Soltanto una condizione al contorno può essere soddisfatta, nessun flusso attraverso il bordo orientale. Una più completa descrizione del flusso richiede equazioni più complete.
4. Le soluzioni non danno informazioni sulla distribuzione verticale della corrente.
5. I Risultati furono basati su dati di due campagne più i dati di vento mediati, assumendo uno stato stazionario. Calcoli posteriori, fatti da Leetma, McCreary, e Moore (1981) usando dati di vento più recenti producono soluzioni con una variabilità stagionale che é in buon accordo con le osservazioni fissando il livello di 'no motion' a 500m. Se si sceglie un'altra profondità, i risultati non sono così buoni.
6. Wunsch (1996: §2.2.3) dopo aver esaminato attentamente il bilancio di Sverdrup nell'Oceano, concluse che non abbiamo abbastanza informazioni per controllare la teoria. Egli scrive

   Il proposito di questa estesa discussione non é stato quello di disapprovare la validità del bilancio di Sverdrup. Piuttosto, é quello di enfatizzare il divario comunemente esistente in oceanografia tra una idea teorica attraente e plausibile e l'abilità di dimostrare la sua applicabilità quantitativa agli attuali flussi oceanici. - Wunsch (1996).

   Wunsch, comunque, fà notare

   Il ragionamento di Sverdrup é così centrale per le teorie di circolazione oceanica che quasi tutte le discussioni assumono esso valido senza ulteriori commenti e procedono a calcolare le sue conseguenze per dinamiche di ordine superiori... é difficile sovrastimare l'importanza del bilancio di Sverdrup - Wunsch (1996).

   Ma il divario é stringente. Le misure dello sforzo medio nel Pacifico equatoriale (Yu and McPhaden, 1999) mostrano che il flusso é nel bilancio di Sverdrup.

Linee di flusso, Linee di cammino e funzioni di flusso
Prima di discutere ulteriormente della circolazione oceanica forzata dal vento, abbiamo bisogno di introdurre il concetto di Linea di flusso e di funzione di flusso, 1990: 51 & 66).

Ad ogni istante del tempo, possiamo rappresentare il campo del flusso in un fluido dal vettore velocità in ogni punto dello spazio. Le curvistantanee che sono ovunque tangenti alla direzione dei vettori sono chiamate lineee di flusso (stream lines). Se il flusso é instabile, le linee di flusso cambiano con il tempo.

La traiettoria di una particella fluida, il cammino seguito da un drifter lagrangiano, é detto linea del cammino in meccanica dei fluidi. La linea del cammino é la stessa della linea di flusso per un flusso stazionario, e sono differenti per un flusso non stazionario.

Possiamo semplificare la descrizione dei flussi bi-dimensionali, incompressibili usando la funzione di corrente y definita da:

(11.11)

La funzione di corrente é usata spesso perché é una quantità scalare da cui é possibile calcolare il vettore del campo della velocità. Questo porta ad equazioni più semplici per alcuni flussi.

Le funzioni di corrente sono utili anche per la visualizzazione del flusso. Ad ogni istante, il flusso é parallelo alle linee di Ψ costante. Così se il flusso é stazionario, le linee di funzione di corrente costanti sono i cammini seguiti dalle particelle di acqua.

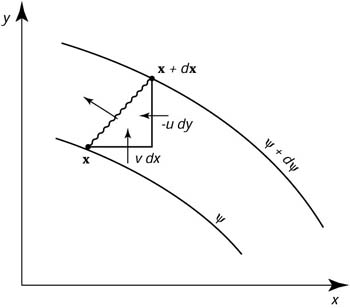Figura 11.4 Trasporto del volume tra linee di corrente in un flusso bi--dimensionale stazionario. Da Kundu (1990).

Il tasso di flusso di volume tra qualunque due linee di corrente di un flusso stazionario é dy, ed il tasso di flusso di volume tra due linee di corrente y₁ e y₂ é uguale a y₁ - y ₂. Per vedere ciò, consideriamo una linea arbitraria dx = (dx, dy) tra due linee di corrente (Figura 11.4). Il tasso di flusso di volume tra le linee é:

(11.12)

ed il tasso volumetrico del flusso tra due linee di corrente é numericamente uguale alla differenza dei loro valori di Ψ.

Ora, applichiamo i concetti alle mappe di topografia oceanica degli altimetri satellitari. Nel §10.3 abbiamo scritto (10.10)

	(11.13)

Comparando la (11.14) con la (11.12) é chiaro che

(11.14)

e la superficie marina é una funzione di corrente scalata da g/f. Tornando alla Figura 10.6, le linee di altezza costante sono linee di corrente, ed il flusso é lungo le linee. Il trasporto geostrofico superficiale é proporzionale alla differenza in altezza, independente dalla distanza tra le linee di corrente. La stessa asserzione é applicata alla Figura 10.9, eccetto che il trasporto é relativo alla superficie di 1000 decibar, che é profonda circa 1000m.

Oltre alla funzione di corrente, gli oceanografi usano la funzione di corrente del trasporto di massa Ψ definita da:

(11.15)

Questa è la funzione mostrata nelle Figure 11.2 e 11.3.

11.2 La Teoria di Stommel sulle Correnti Occidentali

Allo stesso tempo in cui Sverdrup stava cominciando a capire la circolazione del Pacifico orientale, Stommel stava cominciando a capire perché le correnti occidentali di bordo esistevano nei bacini oceanici. Per studiare la circolazione del Nord Atlantico, Stommel (1948) usò essenzialmente le stesse equazioni usate da Sverdrup (11.1, 11.2, and 11.3) ma aggiunse un semplice sforzo al fondo proporzionale alla velocità alla (11.3):

	(11.16a)
	(11.16b)

dove F e R sono costanti.

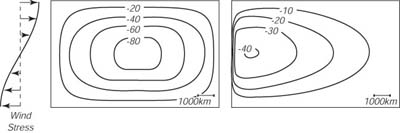
Stommel calcolò le soluzioni stazionarie per un flusso dentro un bacino rettangolare 0 ≤ y ≤ b, 0 ≤ x ≤ λ con profondità costante D riempito con acqua a densità costante. La sua prima soluzione fù per una Terra non rotante. Questa soluzione ha un flusso simmetrico con nessuna corrente occidentale di bordo (Figura 11.5, sinistra). Poi, Stommel assunse una rotazione costante, che di nuovo portava ad una soluzione simmetrica con nessuna corrente occidentale di bordo. Finalmente, assunse che la forza di Coriolis varia con la latitudine. Questo portò ad una soluzione con una intensificazione occidentale (Figura 11.5, destra). Stommel suggerì che l'ammassarsi delle linee di flusso ad occidente indica che far variare la forza di Coriolis con la latitudine può spiegare perché si trova la Gulf Stream nell'Oceano. Ora sappiamo che la variazione di Coriolis é richiesta per l'esistenza della corrente occidentale di bordo e che gli altri modelli per il flusso, che usano differenti formulazione per l'attrito, portano a correnti occidentali di bordo con strutture differenti. Pedlosky (1987, Capitolo 5) dà una descrizione, molto utile, succinta e matematicamente chiara delle varie teorie per le correnti occidentali di bordo.

Figura 11.5 Funzione di corrente per un flusso di bacino calcolato da Stommel (1948). Sinistra: Flusso per un bacino non-rotante e per uno con rotazione costante. Destra: Flusso con rotazione variabile linearmente con la y.

Nel prossimo capitolo, vedremo che i risultati di Stommel possono essere anche spiegati in termini di vorticità; il vento produce un momento torcente (vorticità) orario, che deve essere bilanciato da un momento torcente anti-orario al bordo occidentale.

11.3 La Soluzione di Munk

I lavori di Sverdrup e di Stommel suggeriscono i processi dominanti la circolazione forzata dal vento a livello di bacino. Munk (1950) costruì su queste fondazioni, aggiungendo l'informazione di Rossby (1936) sulla viscosità laterale vorticosa, per ottenere una soluzione della circolazione dentro un bacino oceanico. Munk usò l'idea di Sverdrup del trasporto di massa integrato verticalmente che fluisce sopra uno strato più profondo che non si muove. Questo semplifica il problema matematico ed é più realistico. Le correnti oceaniche sono concentrate nei primi 1000m dell'Oceano, non sono barotropiche e sono independenti dalla profondità. Per includere l'attrito, Munk usò quello laterale vorticoso con valore costante A_H = A_x = A_y. Le equazioni (11.1) diventano:

	(11.17a)
	(11.17b)

Munk integrò le equazioni da una profondità -D alla superficie a z = z₀ che é simile all'integrazione di Sverdrup eccetto che la superficie non é a z = 0. Munk assunse che le correnti alla profondita -D svaniscono e che la (11.3) appicata al bordo orizzontale dalla cima al fondo dello strato, e che A_H é costante.

Per semplificare le equazioni, Munk usò la funzione di corrente del trasporto di massa (11.15), e proseguì lungo le linee di Sverdrup. Eliminò il termine della pressione prendendo la derivata in y della (11.17a) e la derivata in x della (11.17b) per ottenere l'equazione del trasporto di massa:

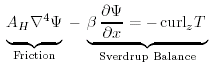(11.18)

dove

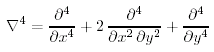(11.19)

é l'operatore bi-armonico. L'equazione (11.18) é la stessa di (11.6) con in più il termine dell'attrito laterale A_H. Il termine dell'attrito é forte vicino al bordo laterale dove le derivate orizzontali del campo della velocità sono grandi ed é piccolo all'interno del bacino oceanico. In questo modo, all'interno, il bilancio delle forze é lo stesso della soluzione di Sverdrup.

L'equazione (11.18) é a derivate parziali di quarto ordine, e sono necessarie quattro condizioni al contorno. Munk assunse il flusso parallelo al bordo e che non ci fosse scivolamento al bordo ?????:

(11.20)

dove n é normale al bordo. Munk allora risolse la (11.18) con la (11.20) assumendo che il flusso fosse in un bacino rettangolare che si estende da x = 0 ad x = r, e da y = -s a y = +s. Egli assunse inoltre che lo sforzo del vento fosse zonale e nella forma:

	(11.21)

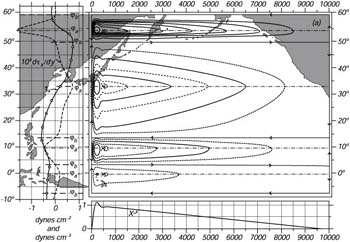
La soluzione di Munk (Figura 11.6) mostra le caratteristiche dominanti della circolazione a scala di gyre di un bacino oceanico. La circolazione é simile a quella di Sverdrup nelle parti orientali del bacino ed una forte corrente occidentale di bordo ad ovest. Usando A_H = 5 × 10³ m²/s dà una corrente di bordo larga circa 225km con una forma simile al flusso osservato nella Gulf Stream e nel Kuroshio.

Figura 11.6 In Alto a Sinistra: lo sforzo del vento medio annuale Tx(y) sopra il Pacifico ed il rotore dello sforzo del vento. jb sono i bordi nord e sud del gyre, dove My = 0 e curl t = 0. j0 é il centro del gyre. In Alto a destra: La funzione di corrente del trasportoo di massa per un bacino rettangolare calcolato da Munk (1950) usando lo sforzo del vento osservato nel Pacifico. L'intervallo tra le isolinee é 10 Sv. Il trasporto totale tra la costa ed ogni punto x, y é y ( x, y ). Il trasporto nella stretta sezione nord é fortemente esagerato. In Basso a Sinistra: Componente nord-sud del trasporto di massa. Da Munk (1950).

Il trasporto nelle correnti occidentali di bordo é independente dalla A_H, e dipende soltanto dalla (11.6) integrata attraverso la larghezza del bacino oceanico. Quindi dipende dalla largezza del bacino, dal rotore dello sforzo del vento, e dal β. Usando la migliore stima disponibile dello sforzo del vento, Munk calcolò che la Gulf Stream doveva avere un trasporto di 36 Sv e che per il Kuroshio era di 39 Sv. I valori sono circa la metà dei valori misurati disponibili a Munk. Questo é in buon accordo, considerando che lo sforzo del vento non era ben conosciuto.

Recenti ricalcoli mostrano un buon accordo eccetto per la regione di Capo Hatteras dove esiste una forte ri-circolazione. La soluzione di Munk fù basata sullo sforzo del vento mediato su quadrati di 5°. Questo sottostimava il rotore dello sforzo. Leetma e Bunker (1978) usarono coefficienti dello sforzo moderni e mediando con 2°×5° ottennero un trasporto di 32Sv per la Gulf Stream, un valore molto vicino a quello calcolato da Munk.

11.4 La Circolazione osservata in Atlantico

Le teorie di Sverdrup, Munk, e Stommel descrivono un flusso molto semplice. Ma l'Oceano é molto più complicato. Per vedere solo come il flusso sia complicato in superficie, guardiamo ad un intero bacino, l'Atlantico settentrionale. Ho scelto questa regione perché é la meglio osservata e perché i processi di media latitudine nell'Atlantico sono simili a quelli di altri oceani. Così, per esempio, usiamo la Gulf Stream come una corrente occidentale di bordo.

Cominciamo dalla Gulf Stream per vedere come la nostra comprensione delle correnti oceaniche si é evoluta. Naturalmente, non possiamo guardare a tutti gli aspetti del flusso. Potete trovare molto di più leggendo il libro di Tomczak e Godfrey (1994) su Regional Oceanography: An Introduction.

La Circolazione del Nord Atlantico
L'Atlantico settentrionale é il più studiato dei bacini. C'é un esteso corpo di teorie per descrivere molti aspetti della circolazione, che include il flusso in superficie, nel termoclino, ed ad ogni profondità, insieme ad un esteso corpo di osservazioni sul posto. Guardando le figure che mostrano la circolazione, possiamo imparare molto sulla circolazione, e guardando le figure prodotte durante le ultime decadi possiamo tracciare una comprensione più completa della circolazione.

Cominciamo con la tradizionale vista del flusso mediato nel tempo, basata principalmente sulle osservazioni idrologiche del campo di densità. (Figura 2.8). é una vista contemporanea della circolazione media dell'intero oceano basata su un secolo di misure. Poiché la figura include tutti gli oceani, forse é troppo semplificata. Allora, guardiamo ad una vista simile della circolazione media del solo Atlantico settentrionale. (Figura 11.7).

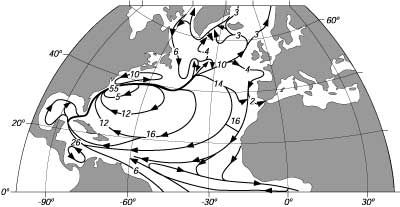
Figura 11.7 Schema delle maggiori correnti di superficie del Nord Atlantico. I valori sono in unità 106m3/s. Da Sverdrup, Johnson, e Fleming (1942: fig. 187).

La figura mostra un grande 'gyre' alle medie latitudine, a scala di bacino, come ce lo aspettiamo descritto dalla teoria di Sverdrup nel §11.1. Ad ovest, una corrente occidentale di bordo, la Gulf Stream, completa il 'gyré. Nel nord un 'gyre' subpolare include la corrente del Labrador. Un sistema di corrente e controcorrente si vede a basse latitudini con un flusso simile a quello del Pacifico. Da notare, comunque, il grosso flusso attraverso l'equatore che scorre lungo la costa nord-est del Brasile verso i Caraibi.

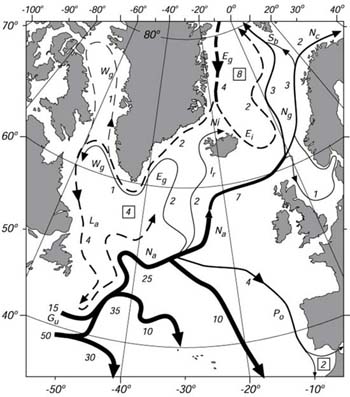
Se guardiamo più da vicino al flusso nel lontano nord Atlantico (Figura 11.8) vediamo che il flusso é ancora più complesso. Questa figura include molti più dettagli di una regione importante per la pesca e per il commercio. Poiché é basata su una imponente base di osservazioni idrologiche, e questa la realta? Per esempio, se lanciamo un drifter lagrangiano nell'Atlantico, seguirà le linee di corrente mostrate nella figura?

Figura 11.8 Schema dettagliato delle correnti in Nord Atlantico che mostra le maggiori correnti superficiali. I numeri danno il trasporto in unità di 106 m3/s dalla superficie ad una profondità di 1000 m. Eg: Corrente di Groenlandia dell'est; Ei: Corrente dell'Islanda dell'est; Gu: Gulf Stream; Ir: Corrente di Irminger; La: Corrente del Labrador; Na: Corrente del Nord Atlantico; Nc: Corrente di Capo Nord; Ng: Corrente Norvegese; Ni: Corrente del Nord Islanda; Po: Corrente del Portogallo; Sb: Corrente dello Spitsbergen; Wg: Corrente della Groenlandia ovest. I numeri dentro i quadri danno l'acqua che affonda in unità di 106m3/s. Linee Piene: Correnti relativamente calde. Linee Trattegiate: Correnti relativemente fredde. Da Dietrich, et al. (1980).

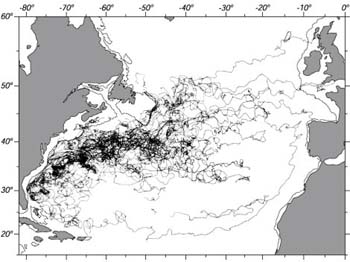
Per rispondere alla domanda, guardiamo alle tracce sulla superficie marina di 110 drifter compilate da Phil Richardson (Figura 11.9 sinistra). Le tracce danno una visione molto differente delle correnti del Nord Atlantico. E' difficile distinguere il flusso da una giungla di linee, talvolta chiamate tracce di spaghetti (spaghetti tracks). Chiaramente, il flusso é molto turbolento, specialmente nella Gulf Stream, una veloce corrente occidentale di bordo. Inoltre, i vortici turbolenti sembrano avere un diametro di pochi gradi. Questo é molto differente dalla turbolenza nell'atmosfera. Nell'aria, i grandi vortici sono chiamati tempeste, e possono avere 10°-20° di diametro. Così le 'tempeste' oceaniche sono molto più piccole di quelle atmosferiche.

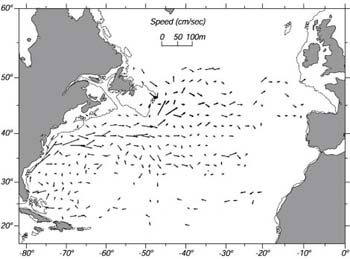
Figura 11.9 Sinistra: Tracciato di 110 drifter lanciati nel nord-ovest dell'Atlantico. Destra: Velocità media delle correnti in riquadri di 2°×2° calcolati dalle tracce di prima. I riquadri con meno di 40 osservazioni sono omessi. La lunghezza delle freccie é proporzionale alla velocità. I valori massimi sono intorno ai 0.6m/s nella Gulf Stream vicino 37°N 71°W. Da Richardson (1981).

Forse possiamo vedere il flusso medio se mediamo le tracce dei drifter. Cosa succede quando Richardson mediò le tracce con scatole da 2°×2° ? Le medie (Figura 11.9 destra) cominciano a mostrare alcuni trend, ma notiamo che in alcune regioni, come ad est della Gulf Stream, riquadri vicini hanno medie molto differenti, alcuni hanno correnti che vanno in direzioni differenti. Questo indica che il flusso é così variabile, che la media non é stabile. Quaranta e più osservazioni non danno un valore medio stabile. Complessivamente, Richardson trovò che l'energia cinetica dei vortici é da 8 a 37 volte più grande di quella del flusso medio. Dunque, la turbolenza oceanica é molto differente da quella del laboratorio. Nel laboratorio, il flusso medio é tipicamente molto più veloce dei vortici.

Un successivo lavoro di Richardson (1993) basato su boe sub-superficiali alla deriva a profondità tra i 500m e i 3500 m, mostra che la corrente si estende a profondità sotto la superficie e che il diametro tipico di un vortice é di 80 km.

La Regione di Ricircolazione della Gulf Stream
Se guardiamo con maggiore attenzione alla Figura 11.7 vediamo che il trasporto della Gulf Stream aumenta da 26Sv nello stretto della Florida (tra la Florida e Cuba) a 55Sv a largo di Capo Hatteras. Misure successive mostrano che il trasporto aumenta da 30Sv nello Stretto di Florida a 150Sv vicino il 40°N.

L'aumento osservato ed il grande trasportoo al largo di Capo Hatteras, é in disaccordo con i trasporti calcolati dalla teoria di Sverdrup. La teoria predice un trasporto massimo di 30Sv che é molto più piccolo, che ha il valore massimo vicino a 38° e che il massimo dovrebbe stare vicino al 28°N. Allora abbiamo un problema: che cosa causa trasporti così alti vicino 40°N?

Niiler (1987) riassunse la teoria e le osservazioni. Primo, non c'é evidenza idrologica di un grande flusso di acqua dalle Corrente delle Antille che fluisce a nord delle Bahamas e nella Gulf Stream. Questo elimina la possibilità che il flusso di Sverdrup sia più grande di quello calcolato e che il flusso gira fuori del Golfo del Messico. Il flusso sembra venire principalmente dalla Gulf Stream stessa. Il flusso tra 60°W e 55°W é diretto a sud. L'acqua quindi fluisce a sud-ovest e si riunisce alla Corrente tra 65°W e 75°W. Così ci sono due 'gyre' sub-tropicali: uno piccolo direttamente a sud della corrente centrato a 65°W, chiamato regione di ri-circolazione della Gulf Stream e il grande 'gyre' forzato dal vento vicino la superficie, come nella Figura 11.8 che si estende fino all'Europa.

La ri-circolazione della Gulf Stream porta da due a tre volte la massa del gyre più largo. I correntometri posizionati nella regione di ri-circolazione mostrano che il flusso si estende fino al fondo. Questo spiega perché la ricircolazione é debole nelle mappe calcolate dai dati idrologici. Le correnti calcolate dalla distribuzione di densità danno solo la componente baroclina del flusso e perdono quella che é independente dalla profondità, la componente barotropica.

La ri-circolazione della Gulf Stream é forzata dall'energia potenziale del termoclino che pende ripidamente nella Gulf Stream. La profondità della superficie di sigma-theta a 27.00 (σ_θ) scende da 250m vicino al 41°N nella Figura 10.8 a 800m vicino al 38°N a sud della corrente. I vortici nella Gulf Stream convertono l'energia potenziale ad energia cinetica attraverso la instabilità baroclina. La instabilità porta ad un fenomeno interessante: la viscosità negativa. La Gulf Stream accelera (non rallenta). Agisce come se fosse sotto l'influenza di una viscosità negativa. Lo stesso processo che porta alla corrente a getto nell'atmosfera. Allo stesso modo, la superficie di densità, che pende fortemente e che separa la massa di aria polare da quella delle medie latitudini nel fronte polare atmosferico, porta ad una instabilità baroclina. Per maggiori dettagli sull'argomento vedi il libro di Starr (1968) su Physics of Negative Viscosity Phenomena.

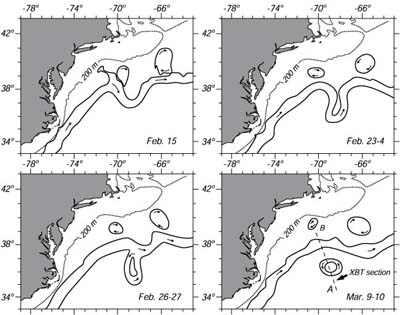
Figura 11.10 I meandri della Gulf Stream portano alla formazione di vortici ruotanti, gli anelli. Notare che gli anelli hanno un diametro di circa 1°. Dal Ring Group (1981).

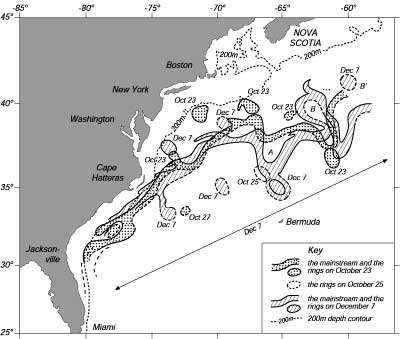
Guardiamo a questo processo nella Gulf Stream (Figura 11.10). Lo shear della forte corrente causa inizialmente al flusso a fare un meandro. Il meandro si intensifica, ed eventualmente stacca un anello dalla corrente. Quelli nel lato sud derivano verso sud-ovest, ed eventualmente si reimmettono nella corrente molti mesi più tardi (Figura 11.11). Il processo avviene lungo tutta la regione di ricircolazione e le immagini da satellite mostrano quasi una dozzina di tali anelli a nord e a sud della corrente (Figura 11.11). Nell'Atlantico meridionale, c'é un'altra corrente occidentale di bordo, la Corrente del Brasile che completa la circolazione in questo bacino. Tra il flusso nel nord e sud Atlantico si colloca la circolazione equatoriale simile a quella del Pacifico. Ora possiamo completare la nostra descrizione della Corrente Circunpolare Antartica.

Figura 11.11 Schema della posizione della Gulf Stream, i vortici a centro caldo e quelli a centro freddo osservati nelle immagini infrarosse della superficie marina misurati con il radiometro infrarosso posto sul NOAA-5 nell'Ottobre e Dicembre 1978. Da Tolmazin (1985: 91).

11.5 Concetti Importanti

1. La teoria per correnti geostrofiche, forzate dal vento, fu per prima deliniata dai lavori di Sverdrup, Stommel, e Munk tra il 1947 ed il 1951.
   
   
2. Essi mostrarono che correnti realistiche possono essere calcolate soltanto se il parametro di Coriolis varia con la latitudine.
   
   
3. Sverdrup mostrò che il rotore dello sforzo del vento guida il trasporto di massa, verso nord e che questo può essere usato per calcolare le correnti nell'oceano lontano dalle correnti occidentali di bordo.
   
   
4. Stommel mostrò che le correnti occidentali di bordo sono richieste per far circolare il flusso in un bacino oceanico quando il parametro di Coriolis varia con la latitudine.
   
   
5. Munk mostrò come combinare le due soluzioni per calcolare la circolazione geostrofica forzata dal vento in un bacino oceanico. In ognuno dei tre casi, la corrente é forzata dal rotore dello sforzo del vento.
   
   
6. La circolazione osservata negli oceani é molto turbolenta. E' necessario mediare insieme molti anni di osservazioni per ottenere una mappa stabile del flusso medio.
   
   
7. La Gulf Stream é una regione di instabilità baroclina in cui la turbolenza accelera la corrente. Questo crea una ricircolazione della Gulf Stream. I trasporti della regione di ricircolazione sono molto più grandi di quelli calcolati dalla teoria di Sverdrup-Munk.