Capitolo 16 - Onde del Mare

Guardando il mare dalla spiaggia, possiamo vedere le onde della superfice marina. Guardando attentamente, notiamo che le onde sono ondulazioni della superfice matina con una altezza di circa un metro, dove l'altezza e' la distanza verticale tra il punto piu' basso del cavo e la cima della cresta vicina. .La lunghezza dell'onda, che possiamo prendere come la distanza tra due creste successive, e' tra 50-100 m. Osservando le onde per pochi minuti, possiamo notare che l'altezza e la lunghezza delle onde non sono costanti. Le altezze variano casualmente sia nel tempo che nello spazio, e le propieta' statistiche delle onde, come l'altezza media osservata per un centinaio di onde, cambia da giorno a giorno. Queste onde provenienti dal largo sono generate dal vento. Qualche volta i venti locali generano onde, altre volte sono le tempeste lontane che generano le onde che alla fine raggiungono la costa. Per esempio, le onde che si rompono sulla costa della California del sud durante una giornata estiva possono venire da una vasta tempesta al largo dell'Antartide, distante 10000 km.

Se guardiamo piu' da vicino e per lungo tempo, notiamo che il livello del mare cambia di ora in ora. Durante un periodo di una giornata, il livello del mare descresce rispetto ad un livello fisso sulla spiaggia di circa un metro. Il lento salire e scendere del livello marino e' dovuto alle maree, un altro tipo di onda superficiale marina. Le maree hanno lunghezze di onda di migliaia di kilometri, e sono generate dai cambiamenti lenti e molto piccoli della gravita' dovuti al moto della Terra relativo alla Luna ed al Sole.

In questo capitolo descriveremo quantitativamente le onde superficiali dell'Oceano. Nel successivo capitolo descriveremo le onde lungo la costa e la marea.

16.1 La Teoria Lineare delle Onde Superficiali Oceaniche

Le onde superficiali sono intrinsecamente non-lineari: la soluzione delle equazioni del moto dipendono dalle condizioni al contorno sulla superfice, ma le condizioni alla superfice di contorno sono propio le onde che desideriamo calcolare. Come possiamo procedere?

Cominciamo assumendo che l'ampiezza delle onde alla superfice dell'acqua e' infinitamente piccolo cosi' la superfice e' quasi esattamente un piano. Per semplificare la matematica, possiamo assumere che il flusso e' bi-dimensionale con le onde che viaggiano nella direzione della x. Assumiamo anche che la forza di Coriolis e la viscosita' puo' essere trascurata. Se manteniamo la rotazione, abbiamo le onde di Kelvin discusse nel §14.2.

Con queste assunzioni, l'elevazione della superfice marina z di un'onda che viaggia nella direzione x e':

con

(16.2)

dove ω e' la frequenza dell'onda in radianti al secondo, f e' la frequenza dell'onda in Hertz (Hz), k e' il numero d'onda, T e' il periodo dell'onda, L e' la lunghezza d'onda, e dove assumiamo, come stabilito prima, che k a = O (0).

Il periodo dell'onda T e' il tempo che passa tra due successive creste delle onde ad un punto fisso. La lunghezza dell'onda L e' la distanza tra due successive creste delle onde o cavi ad un determinato tempo.

La Relazione di Dispersione
La frequenza dell'onda w e' legata al numero d'onda k dalla relazione di dispersione (Lamb, 1932 §228):

dove d e' la profondita' dell'acqua e g e' l'accelerazione di gravita'.

Due approssimazioni sono particolarmente utili.

1. Approssimazione di Acqua Profonda e' valida se la profondita' dell'acqua d e' molto piu' grande della lunghezza d'onda L. In questo caso, d >> L, kd >> 1, e tanh (kd) = 1.

2. approssimazione di Acqua poco profonda e' valida se la profondita' dell'acqua e' molto meno della lunghezza d'onda. In questo caso, d << L, kd << 1, e tanh (kd) = kd.

Per questi due limiti della profondita' dell'acqua comparati con la lunghezza la relazione di dispersione si riduce a:

I limiti stabiliti per d/L da' una relazione di dispersione accurata entro il 10%. Poiche' molte propieta' delle onde possono essere misurate con una accuratezza di 5-10%, le approssimazioni sono utili per calcolare le propieta' delle onde. Piu' tardi impareremo a calcolare le propieta' delle onde quando le onde si propagano da acque profonde a quelle basse.

Velocita' di Fase
La velocita' di fase c e' la velocita' a cui una particolare fase dell'onda si propaga, per esempio, la velocita' di propagazione della cresta dell'onda. In un periodo dell'onda T la cresta si sposta di una lunghezza d'onda L e la velocita' di fase c = L/T = ω/k. Cosi', la definizione della velocita' di fase e':

(16.6)

La direzione di propagazione e' perpendicolare alla cresta dell'onda e verso la direzione positiva della x. Le approssimazioni di acqua profonda e bassa per la relazione di dispersione danno:

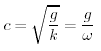	Velocita' di Fase per Acqua Profonda	(16.7)
	Velocita' di Fase per acqua poco profonda	(16.8)

Le approssimazioni sono accurate a circa 5% dei limiti stabiliti nelle (16.4, 16.5).

Nelle acque profonde, la velocita' di fase dipende dalla lunghezza o dalla frequenza delle onde. Le onde piu' lunghe viaggiano piu' veloci. Cosi', le onde di acqua profonda sono dispersive. In acque poco profonde, la velocita' di fase e' independente dalle onde; questo dipende soltanto dalla profondita' dell'acqua. Le onde di acqua poco profonda sono non-dispersive.

Velocita' di Gruppo
Il concetto di velocita' di gruppo c_g e' fondamentale per comprendere la propagazione delle onde lineari e non-lineari. Primo, e' la velocita' a cui un gruppo di onde viaggia attraverso l'oceano. Piu' importante, e' anche la velocita' di propagazione dell'energia. Whitham (1974, §1.3 e §11.6) da' una chiara derivazione del concetto e della fondamentale equazione (16.9).

La definizione della velocita' di gruppo in due dimensioni e':

(16.9)

Usando le approssimazioni per la relazione di dispersione:

	Velocita' di Gruppo in Acqua Profonda	(16.10)
	Velocita' di Gruppo per Acqua Poco Profonda	(16.11)

Per le onde superficiali del Mare, la direzione di propagazione e' perpendicolare alla creste delle onde nella dirazione positiva dell'asse x. Piu' in generale, negli altri tipi di onde, come nelle onde di Kelvin e di Rossby incontrate nel §14.2, la velocita' di gruppo non e' necessariamente nella direzione perprndicolare alle creste delle onde.

Notare che un gruppo di onde in acqua profonda si muove a meta' della velocita' di fase delle onde che formano il gruppo. Come puo' succedere? Se potessimo osservare piu' da vicino un gruppo di onde, potremmo vedere le creste delle onde apparire in fondo al treno di onde, le creste muoversi lungo il treno e scomparire nella parte iniziale del gruppo.

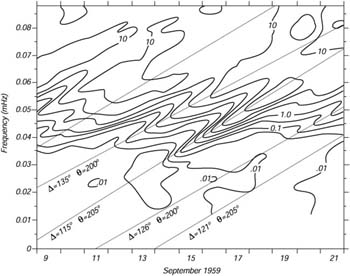
Ogni cresta dell'onda si muove al doppio della velocita' di gruppo. Le onde del mare che si muovono realmente nel mare sono governate dalla relazione di dispersione? Si! Walter Munk e colleghi (1963) in una serie di ragguardevoli esperimenti fatti negli anni 60', mostrarono che le onde dell'Oceano che si propagano su grandi distanze sono dispersive, e che la dispersione poteva essere usata per tracciare le tempeste. Le onde furono registrate per molti giorni usando una griglia di sensori di pressione al largo dell'isola di San Clemente, 60 miglia ad ovest di San Diego, California. Gli spettri delle onde furono calcolati per i dati di ogni giorno (il concetto di spettro e' discusso nei prossimi paragrafi).Dagli spettri, furono calcolati la direzione di propagazione, le ampiezze e le frequenze delle onde a bassa frequenza. Infine, i contorni dell'energia delle onde furono tabulati in un diagramma tempo-frequenza come nella Figura 16.1.

Figura 16.1 Isolinee dell'energia delle onde, disegnate su un diagramma frequenza-tempo, calcolate dagli spettri delle onde misurate da sensori di pressione al largo della California del sud. Le creste di alta energia delle onde mostrano l'arrivo di treni d'onda disperse da tempeste lontane. La pendenza delle creste e' inversamente proporzionale alla distanza dalla tempesta. Δ e' la distanza in gradi, θ e' la direzione di arrivo delle onde in California. Da Munk et al. (1963).

Per capire la figura, consideriamo una tempesta lontana che produce le onde di molte frequenze. Le onde con la piu' frequenza piu bassa (il w piu' piccolo viaggiano piu' veloci, vedi 16.11), e arrivano prima delle altre onde, con fequenza piu' alta. Piu' lontana e' la tempesta, piu' e' grande il ritardo dell'arrivo delle varie frequenze. Le creste di alta energia delle onde visti nella Figura sono prodotti dalle singole tempeste θ. La pendenza delle creste fornisce la distanza dalla tempesta in gradi Δ lungo un grande cerchio; e la informazione della fase dalla griglia fornisce l'angolo di provenienza della tempesta. I due angoli danno il luogo di origine relativo a San Clemente. In tal modo, le onde che arrivano dal 15 al 18 Settembre producono una cresta che ci da' la tempesta lontana 115° ad un angolo di 205° che e' circa a sud della Nuova Zealanda vicino all'Antartide.

Le posizioni delle tempeste che producono le onde registrate da giugno ad ottobre 1959 furono comparate con le posizioni delle tempeste riportate dalle mappe meteorologiche ed in molti casi le cose conbaciavano bene.

L'Energia delle Onde
L'energia delle onde E espressa in Joule per metro quadro e' relazionata alla varianza dello spostamento della superfice marina ζ dalla:

dove ρw e' la densita' dell'acqua, g e' la gravita', e le parentesi denotano la media nel tempo o nello spazio.

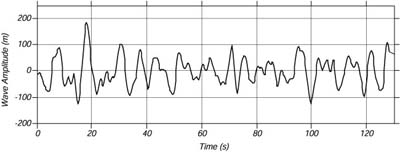
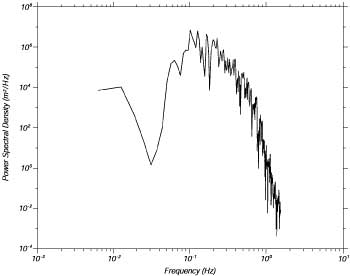
Figura 16.2 Una breve registrazione dell'ampiezza delle onde misurate da una boa ondametrica nel Nord Atlantico.

Altezza Significativa dell'Onda
Cosa vogliamo dire con altezza dell'onda? Se guardiamo ad un mare forzato dal vento, vediamo onde di varia altezza. Alcune sono molto piu' grandi di altre (Figura 16.2). Una definizione pratica molto usata e' quella di 1/3 delle onde piu' alte, H_1/3. L'altezza e' calcolata come segue: si misura l'altezza delle onde per pochi minuti, prendendo circa 120 creste di onde e registrando le loro altezze. Si scelgono le 40 altezze piu' grandi e si calcola la loro media.Questa e' la H_1/3 della registrazione delle onde.

Il concetto di altezza significativa fu sviluppato durante la Seconda Guerra Mondiale come parte di un progetto per la previsione delle altezza e dei periodi delle onde. Wiegel (1964: p. 198) riporta quel lavoro allo Scripps Institution of Oceanography e dice:

...L'altezza delle onde stimata dagli osservatori corresponde alla media del 20-40 per cent delle onde piu' alte... Originalmente, il termine altezza dell'onda significativa era allegato alla media di queste osservazioni, il 30 per cento delle onde piu' alte, si e' evoluto fino a diventare la media di un terzo delle onde piu' alte, (denominato H_S or H_1/3 )

Piu' recentemente, l'altezza dell'onda significativa e' calcolato dallo spostamento della superfice misurata. Se il mare contiene un intervallo stretto di frequenze, H_1/3 e' relazionato alla deviazione standard dello spostamento del livello marino (NAS, 1963: 22; Hoffman and Karst, 1975).

dove < ζ ² > ^1/2 e' la deviazione standard dello spostamento della superfice. Questa relazione e' molto piu' utile, ed e' ora il modo accettato per calcolare l'altezza delle onde da una misura di onde.

16.2 Onde Non-Lineari

Abbiamo derivato le propieta' delle onde superficiali del mare assumendo che le onde siano infinitamente piccole k a = O (0). Se le onde sono k a << 1 ma non infinitamente piccole, le propieta' delle onde possono essere espanse in una serie di potenze di k a (Stokes, 1847). Stokes calcolo' la propieta' di un'onda con ampiezza finita e trovo':

(16.14)

Le fasi delle componenti della serie di Fourier per l'espanzione della ζ nella (16.14) sono tali che le onde non-lineari hanno creste scoscese e cavi piatti. La massima ampiezza delle onde di Stokes e' a_max = 0.07 L (k a = 0.44). Queste onde ripide in acque profonde sono chiamate onde di Stokes (Vedi anche Lamb, 1945, §250).

La conoscenza delle onde non-lineari aumento' lentamente fino a quando Hasselmann (1961, 1963a, 1963b, 1966), usando gli strumenti della fisica delle particelle ad alta energia, risolse fino al sesto ordine le interazioni di tre o piu' onde della superfice marina. Hasselman, Phillips (1960), e Longuet-Higgins e Phillips (1962) mostrarono che n onde libere sulla superfice del mare possono interagire per produrre un'altra onda libera soltanto se le frequenze ed i numeri d'onda delle onde che interagiscono hanno somma zero:

dove permettiamo alle onde di viaggiare in ogni direzione, e k _i e' il vettore del numero d'onda, che fornisce la lunghezza e la direzione dell'onda. Le (16.15a, b) sono i requisiti generali per tutte le onde che interagiscono.
(The fewest number of waves that meet the conditions of (16.15))
sono tre onde che interagiscono per produrre una quarta. L'interazione e' debole; le onde devono interagire per centinai di lunghezze d'onda e periodi per produrre la quarta onda con un'ampiezza comparabile alle onde che interagiscono. Le onde di Stokes non seguono i criteri delle (16.15) e le componenti dell'onda non sono libere; Le armoniche piu' alte sono limitate alle onde primarie.

Il Momento delle Onde
Il concetto di momento dell'onda ha causato considerevole confusione (McIntyre, 1981). In generale, le onde non hanno momento, un flusso di massa, ma hanno un flusso di momento. Questo e' vero per le onde di superfice marina. Ursell (1950) mostro' che un'onda lunga in una Terra roteante non ha trasporto di massa. La sua prova sembra contraddire le usuali discussioni dei libri di testo su onde non-lineari, ripide come quelle di Stokes. Le particelle di acqua in un'onda di Stokes si muove lungo una traiettoria che e' quasi circolare, ma non si chiude, e la particella si muove lentamente nella direzione di propagazione dell'onda. Questo e' transporto di massa, ed il fenomeno e' detto deriva di Stokes. Ma il transporto in avanti, vicino la superfice, e' bilanciato da un eguale trasporto nella direzione opposta in profondita', e non c'e' un flusso di massa netto.

Onde Solitarie (Solitoni)
Le onde solitarie sono un'altra classe di onde non-lineari, ed hanno propieta' molto interessanti. Si propagano senza cambiare la forma, e due solitoni possono incrociarsi senza interazione. Il primo solitone fu scoperto da John Scott Russell (1808-1882), che segui' un'onda solitaria generata da una barca nello Union Canal di Edinburgo nell'anno 1834.

Scott fu' testimone di una tale onda mentre osservava una barca che era tirata da una coppia di cavalli lungo lo Union Canal. Quando la barca si fermo', noto' che l'acqua attorno al natante si sollevo' in avanti in una forma di una singola onda, la cui altezza e velocita' rimaneva virtualmente invariata. Russell insegui' con un cavallo l'onda per piu' di un miglio prima di ritornare a casa per ricostruire l'evento nella vasca sperimentale del suo giardino. - Nature 376, 3 August 1995: 373.

Le propieta' delle onde solitarie risultano da un bilancio esatto tra la dispersione che tende a distribuire l'onda solitaria in un treno di onde, ed effetti non-lineari che tendono ad accorciare e ad inclinare l'onda. Il tipo di onda solitaria in acqua bassa visto da Russell, prende la forma:

(16.16)

che si propaga alla velocita':

(16.17)

Si puo' pensare che tutte le onde di acqua poco profonda sono dei solitoni perche' sono non-dispersive, e quindi si dovrebbero propagare senza cambiare forma. Sfortunatamente, questo non e' vero se le onde hanno una ampiezza finita. La velocita' delle onde dipende dalla profondita'. Se l'onda consiste di una singola gobba, allora l'acqua della cresta viaggia piu' veloce di quella nel cavo, e l'onda si inclina quando si muove in avanti, Alla fine, l'onda diventa molto ripida e si rompe. A quel punto e' chiamata mascaretto (bore). In alcune bocche di fiume l'alta marea e' cosi' alta e l'estuario cosi' lungo e poco profondo che l'onda di marea entrando nell'estuario si innalza e si rompe producendo un mascaretto che risale lungo il fiume. Questo accade nel Rio delle Amazzoni in Sud America, nel Severn in Europa e nello Tsientang in Cina (Pugh, 1987: 249).

16.3 Le Onde ed il Concetto di Spettro delle Onde

Se guardiamo il mare, notiamo che le onde sulla superfice marina non sono semplici sinusoidi. La superfice appare composta da onde senza un ordine con varie lunghezze e periodi. Come possiamo descrivere questa superfice? la semplice risposta e': Non molto facilmente. Possiamo, comunque, con alcune semplificazioni, andare ad una descrizione piu' precisa della superfice. Le semplificazioni portano al concetto di spettro delle onde marine. Lo spettro fornisce la distribuzione dell'energia delle onde tra le differenti frequenze delle lunghezze delle onde sulla superfice marina.

Il concetto di spettro e' basato sul lavoro di Joseph Fourier (1768 - 1830), il quale mostro' che ogni funzione ζ (t) (or ζ (x) se volete), puo' essere rappresentata nell'intervallo -T/2 < t < T/2 come la somma di una serie infinita di funzioni seno e coseno con frequenze d'onda armoniche:

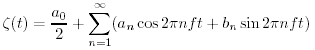(16.18)

dove

	(16.19a)
	(16.19b)

f = 1/T e' la frequenza fondamentale, e nf sono le armoniche della frequenza fondamentale. Questa forma della ζ (t) e' detta serie di Fourier (Bracewell, 1986: 204; Whittaker e Watson, 1963: §9.1). Notare che a₀ e' il valore medio della ζ (t) dell'intervallo considerato.

Le equazioni (16.18 e 16.19) possono essere semplificate usando

(16.20)

dove i = radice quadrata di (-1). Le equazioni (16.18 e 16.19) allora diventono:

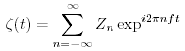(16.21)

where

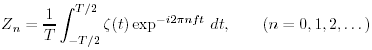(16.22)

Z_n e' detta trasformata di Fourier di ζ (t).

Lo spettro S(f) di ζ (t) e':

(16.23)

dove Z* e' la complessa coniugata di Z. Useremo queste forme per le serie di Fourier e gli spettri quando descriviamo il calcolo degli spettri delle onde oceaniche.

Possiamo espandere l'idea delle serie di Fourier per includere le serie che rappresentano le superfici ζ (x, y) usando tecniche simili. In tal modo, ogni superfice puo' essere rappresentata come una serie infinita di funzioni di seni e coseni orientata in tutte le direzioni possibili.

Ora, applichiamo queste idee alla superfice marina. Supponiamo per un momento che la superfice del mare sia ferma nel tempo. Usando la espansione di Fourier, la superfice congelata puo' essere rappresentata come una serie infinita di funzioni seno e coseno di numeri d'onda differenti orientate in tutte le possibili direzioni. Se scongeliamo la superfice e la lasciamo evolvere nel tempo, possiamo rappresentare la superfice marina come una serie infinita di funzioni seno e coseno di differenti lunghezze d'onda che si muovono in tutte le direzioni. Poiche' le lunghezze d'onda e le frequenze delle onde sono collegate attraverso la relazione di dispersione, possiamo rappresentare la superfice marina anche come una somma infinita di funzioni seno e coseno di frequenza differente in tutte le direzioni.

Notare che nella nostra discussione delle serie di Fourier series assumiamo costanti i coefficienti (a_n, b_n, Z_n). Per tempi di circa un'ora e distanze di dieci kilometri, le onde sulla superfice marina sono abbastanza stabili da ritenere l'assunzione vera. Inoltre, le interazioni non-lineari tra le onde sono deboli. Quindi, possiamo rappresentare la superfice marina locale come una sovrapposizione lineare di onde sinusoidali aventi molte lunghezze d'onda differenti oppure frequenze e fasi differenti che viaggiano in direzioni diverse. Le serie di Fourier series questa conveniente espressione matematica, stabilisce che la superfice marina e' veramente composta di onde sinosuidali, ognuna propagantesi in accordo alle equazioni scritte nella §16.1.

Il concetto di superfice marina composta da onde indipendenti puo' essere ulteriormente esteso. Supponiamo di gettare un sasso in un mare a riposo, e di fare un bel tonfo. In accordo a Fourier, il tonfo puo' essere rappresentato come una sovrapposizione di coseni quasi tutti con fase zero cosi' le onde si sommano per il grande tonfo all'origine. Dopo di che, ogni singola onda di Fouriern comincia a viaggiare allontanandosi dal tonfo iniziale. Le onde piu' lunghe viaggiano piu' veloci, ed eventualmente, lontano dal tonfo, il mare consiste di un treno disperso di onde con le piu' lunghe lontane e le piu' corte vicine. Questo e' asattamente quello che vediamo nella Figura 16.1.La tempesta fa' il tonfo, e le onde si disperdono come visto nella figura.

Campionando la Superfice Del Mare
Calcolare le serie di Fourier serie che rappresentano la superfice marina, e' forse impossibile.Cio' richiede che misuriamo l'altezza della superfice del mare ζ (x, y, t) ovunque in un'area di circa dieci kilometri di lato e per un'ora. Dobbiamo semplificare. Supponiamo di installare uno strumento da qualche parte dell'oceano dove registriamo le altezze della superfice marina in funzione del tempo ζ (t). Dovremmo ottenere una registrazione come quella della Figura 16.2. Tutte le onde della superfice marina dovrebbero essere misurate, ma non sappiamo nulla sulla direzione delle onde. Questo e' una misura molto piu' pratica, e ci fornisce lo spettro di frequenza delle onde sulla superfice del mare.

Lavorando con una traccia dell'altezza delle onde, diciamo su un pezzo di carta, e' difficile, cosi' digitizziamo l'uscita dello strumento che misura le altezze, per ottenere

(16.24)

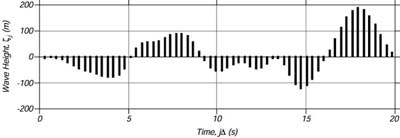
Figura 16.3 I primi 20 secondi dei dati digitalizzati della Figura 16.2. D = 0.32s.

Notare che ζ_j non e' la stessa di ζ (t). We have absolutely no information about the height of the sea surface between samples. Thus we have converted from an infinite set of numbers which describes ζ (t) to a finite set of numbers which describe ζ_j. By converting from a continuous function to a digitized function, we have given up an infinite amount of information about the surface.

L'intervallo di campionamento Δ definisce una frequenza critica di Nyquist (Press et al., 1992: 494)

La frequenza critica di Nyquist e' importante per due ragioni collegate, ma distinte. Una e' una buona notizia, l'altra e' cattiva. Prima la buona notizia. E' un fatto rimarchevole conosciuto come teorema del campionamento: Se una funzione continua z(t) , campionata ad un intervallo Δ, ha una larghezza di banda limitata alle frequenze piu' piccole in grandezza alla Ny, per esempio, se S(nf) = 0 per tutte le |nf| > Ny, allora la funzione z(t) e' completamente determinata dai suoi campioni z_j ... Questo e' un teorema notevole per molte ragioni, tra cui il fatto che il "contenuto di informazione" di una funzione con banda limitata (bandwidth limited function) e', in un certo senso, infinitamente piu' piccola di quella generale e continua...

Ora la notizia cattiva.I'aspetto negativo concerne l'effetto di campionare una funzione continua che non e' limitata a meno della frequenza critica di Nyquist. In quel caso, ne segue che tutta la densita' spettrale che sta' fuori dell'intervallo -Ny < nf < Ny e' erroneamente riportato in quel range. Questo feenomeno e' chiamato scalettamento (aliasing). Ogni componente di frequenza fuori dell'intervallo (-Ny, Ny ) e' 'aliasing' (falsamente spostato) dentro l'intervallo dal processo di campionamento discreto... C'e' poco da fare per rimuovere la potenza traslata una volta che si e' campionato il segnale. Il modo per superare il problema e' (i) conoscere il limite naturale della banda del segnale - oppure forzarlo ad un limite conosciuto filtrando il segnale continuo, e quindi (ii) campionare ad un intervallo di tempo sufficientemente rapido per avere due valori al ciclo della frequenza piu' alta presente nel segnale. - Press et al., 1992, ma con la notazione differente dalla nostra.

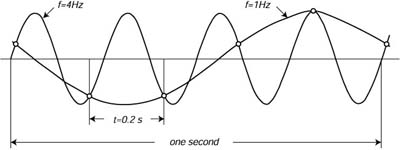
LA FigurA 16.4 illustra il problema del 'aliasing'. Notare come un segnale ad una frequenza e' traslato in una frequenza piu' bassa se la frequenza di origine e' piu' alta della frequenza critica. Fortunatamente, possiamo facilmente evitare il problema: (i) usiamo strumenti che non rispondono alle onde corte ad alta frequenza se siamo interessati alle onde lunghe; e (ii) scegliamo Dt abbastanza piccolo da perdere solo poca informazione. Nell'esempio mostrato in Figura 16.3, nel segnale non ci sono onde da digitalizzare con frequenze piu' alte di Ny = 1.5625 Hz.

Figura 16.4 Campionando un'onda di 4 Hz sinusoidale (linea grossa) ogni 0.2 s si misura una frequenza ad 1 Hz (line sottile). La frequenza critica e' 1 / (2 X 0.2 s) = 2.5 Hz, che e' minore di 4 Hz.

Riassumendo, i segnali digitalizzati dal misuratore di onde non possono essere usati per studiare onde con frequenze piu' alte della frequenza critica di Nyquist. Ne' il segnale puo' essere usato per studiare onde con frequenze piu' basse di quella fondamentale determinata dalla durata della registrazione T delle onde. La registrazione delle onde digitalizzate contengono informazioni nell'intervallo di frequenze:

(16.27)

dove T = NΔ e' la lunghezza della serie temporale, e f e' la frequenzaq in Hertz.

Il Calcolo dello Spettro delle Onde
La trasformata digitale di Fourier Z_n di una registrazione di onde ζ_j equivalente alle (16.21 e 16.22) e':

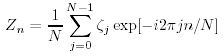	(16.27a)
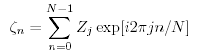	(16.27b)

per j = 0, 1, · · · , N - 1; n = 0, 1, · · · , N - 1. Queste equazioni possono essere calcolate molto velocemente usando La 'Fast Fourier Transform' (FFT), specialmente se N e' una potenza di 2 (Cooley, Lewis, e Welch, 1970; Press et al., 1992: 542).

Il semplice spettro S_n di ζ, che e' chiamato il periodogramma, e':

(16.28)

dove S_N e' normalizzata in modo che:

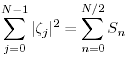(16.29)

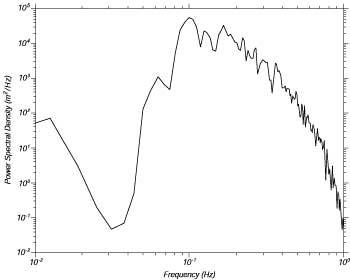
cosi' la varianza di ζ_j e' la somma di (N/2 + 1) termini nel periodogramma. Notate, i termini della S_n sopra la frequenza (N/2) sono simmetrici a quella frequenza. La Figura 16.5 mostra il periodogramma della serie temporale mostrato nella Figure 16.2.

Figura 16.5 Il periodogramma calcolato dai primi 164s di dati della Figure 16.2. La frequenza di Nyquist e' 1.5625Hz.

Il periodogramma e' una funzione con molto rumore. La varianza di ogni punto e' uguale al valore aspettato a quel punto. Dal mediare insieme 10-30 periodogrammi possiamo ridurre l'incertezza del valore ad ogni frequenza. Il periodogramma medio e' chiamato spettro delle altezze della superfice marina (Figura 16.6). Fornisce la distribuzione della varianza delle altezze al misuratore di onde in funzione delle frequenza. Poiche' l'energia delle onde e' proporzionale alla varianza (16.12) lo spettro e' detto lo spettro di energia o lo spettro dell'altezza delle onde. Tipicamente tre ore di dati del misuratore di onde sono usati per calcolare uno spettro di altezza di onde.

Figura 16.6 Lo spettro delle onde calcolato da 11 minuti di dati mostrati nella Figura 7.2 mediando quattro periodogrammi per ridurre l'errore nei valori spettrali. I valori dello spettro inferiori a 0.04Hz sono in errore dovuto al rumore.

Riassunto
Possiamo riassumere i calcoli dello spettro nei seguenti passi:

1. Digitalizzare un segmento dei dati di altezza delle onde per ottenere limiti utili in accordo alla (16.26). Per esempio, usare 1024 valori da 8.53 minuti di dati campionati a 2 valori/secondo.
2. Calcolare la trasformata veloce di Fourier (FFT) Z_n della serie temporale.
3. Calcolare il periodogramma S_n dalla somma dei quadrati delle parti reali e immaginarie della trasformata di Fourier.
4. Ripetere per produrre M = 20 periodogrammi.
5. Mediare i 20 periodogrammi per produrre uno spettro mediato S_M.
6. S_M ha valori che sono χ ² distribuiti con 2M gradi di liberta'.

Questo riassunto del calcolo di uno spettro ignora molti dettagli. Per una informazione piu' completa vedere, per esempio, Percival e Walden (1993), Press et al., (1992: §12), Oppenheim e Schafer (1975), o altri testi sul processamento dei segnali digitali.

16.4 Gli Spettri delle Onde del Mare

Le Onde del Mare sono prodotte dal vento. Piu' forte il vento, piu' a lungo il vento soffia, e piu' vasta l'area sopra cui il vento soffia, piu' grandi saranno le onde. Nel progettare le navi o le strutture marine vorremmo sapere l'altezza dell'onda piu' grande prodotta ad un dato vento. Supponiamo che il vento soffia a 20 m/s per molti giorni su una vasta area del Nord Atlantico. Quale sara' lo spettro delle onde oceaniche nel lato sottovento dell'area?

Lo Spettro di Pierson-Moskowitz
Vari spettri idealizzati sono stati usati per rispondere alla domanda in oceanografia e ingegneria navale. Forse il piu' semplice e' quello proposto da Pierson e Moskowitz (1964). Loro assumono che se il vento ha soffiato costantemente per un "lungo tempo" su una "vasta area", le onde dovrebbero essere in equilibrio con il vento. Questo e' il concetto di mare completamente sviluppato (fully developed sea). Qui, per "lungo tempo" intendiamo circa dieci-mila periodi di onda, e per "vasta area" cinque-mila lunghezze d'onda di lato.

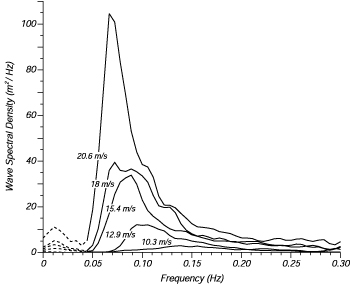
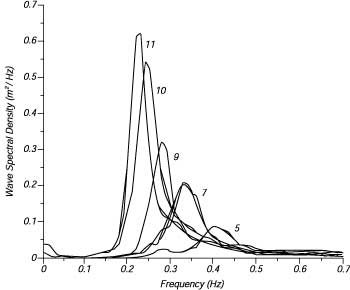
Figura 16.7 Spettri di Onde di un mare completamente sviluppato per differenti velocita' del vento in accordo con Moskowitz (1964).

Per ottenere lo spettro di un mare completamente sviluppato, usarono misure di onde fatte da accelerometri montati sulle navi meteorologiche britanniche nel Nord Atlantico. Prima, selezionarono i dati delle onde per le volte che il vento aveva soffiato costantemente su aree vaste del Nord Atlantico. Poi, calcolarono lo spettro delle onde per le varie velocita' del vento, e trovarono che lo spettro era della forma come nella (Figure 16.7):

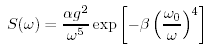(16.30)

dove ω = 2 πf, f e' la frequenza dell'onda in Hertz, a = 8.1 × 10^-3, b = 0.74, ω₀ = g/U_19.5 e U_19.5 e' la velocita' del vento ad una altezza di 19.5 m sopra la superfice marina, l'altezza degli anemometri delle navi meteorologiche usati da Pierson and Moskowitz (1964).

Per la maggior parte del flusso d'aria sopra il mare, lo strato limite atmosferico ha una stabilita' quasi neutra, e

assumendo un coefficiente di attrito di 1.3 × 10^-3.

La frequenza del picco dello spettro di Pierson-Moskowitz e' calcolata dal risolvere dS/dω = 0 per ω_p, per ottenere

La velocita' delle onde al picco e' calcolata da (16.10), che da':

(16.33)

Quindi le onde con frequenza ω_p viaggiano 14% piu' veloci del vento misurato ad una altezza di 19.5 m o 17% piu' veloci del vento misurato ad una altezza di 10 m. Questo pone un difficile problema: Come puo' un vento produrre onde che viaggiano piu' veloci del vento? Tornrremo su questo problema dopo aver discusso lo spettro JONSWAP e l'influenza delleinterazioni non-lineari tra onde generate dal vento.

L'altezza significatifa dell'onda e' calcolata dall'integrale di S(ω) per ottenere:

(16.34)

Ricordando che H_1/3 = 4 <ζ ²>^1/2, l'altezza significant dell'onda calcolata dallo spettro di Pierson-Moskowitz e':

(16.35)

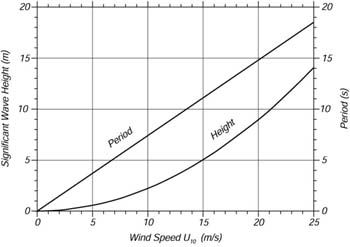
Figura 16.8 fornisce l'altezza significativa ed il periodo dell'onda calcolata dallo spettro di Pierson-Moskowitz.

Figura 16.8 Altezza significativa e periodo dell'onda al picco dello spettro di un mare completamente sviluppato, calcolato dallo spettro di Pierson-Moskowitz usando (16.35 e 16.32).

Figura 16.9 Spettri delle onde di un mare che si sviluppa per differenti "fetch" secondo Hasselmann et al., (1973).

Spettri di JONSWAP
Hasselmann et al., (1973), Dopo aver analizzato i dati raccolti durante il progetto Joint North Sea Wave Observation Project (JONSWAP), trovarono che lo spettro delle onde non e' mai completamente sviluppato. Il mare continua a svilupparsi attraverso interazioni non-lineari onda-onda, anche dopo molto tempo e lunghe distanze. Quindi Loro proposero uno spettro nella forma di (Figura 16.9):

	(16.36a)
	(16.36b)

I dati di onde raccolti durante l'esperimento JONSWAP furono usati per determinare i valori delle costanti della (16.36):

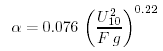	(16.37a)
	(16.37b)
	(16.37c)
	(16.37d)

dove F e' la distanza sottovento, chiamata il fetch, o la distanza sulla quale il vento soffia con velocita' costante.

L'energia delle onde aumenta con il "fetch":

(16.38)

dove x e' il "fetch".

Lo spettro JONSWAP e' simile a quello di Pierson-Moskowitz eccetto che le onde continuano a crescere con la distanza (o il tempo) come specificato dal termine α, ed il picco nello spettro e' piu' pronunciato, come specificato dala termine γ. Quest'ultima risulta particolarmente importante perche' porta ad aumentare le interazioni non-lineari e ad uno spettro che cambia nel tempo in accordo alla teoria di Hasselmann (1966).

La Generazione delle Onde dal Vento
Abbiamo visto negli ultimi pochi paragrafi come le onde sono collegate al vento. Abbiamo, comunque, rinviato fino ad ora come sono generate dal vento. Supponiamo di cominciare con un mare come uno specchio ( scala Beaufort 0). Che cosa succede se improvvisamente il vento comincia a soffiare costantemente, diciamo a 8 m/s?
Tre processi fisici differenti cominciano:

1. La turbolenza nel vento produce fluttuazioni casuali nella pressione alla superfice del mare, che producono piccole onde con lunghezza di pochi centimetri (Phillips, 1957).
2. Dopo, il vento agisce sulle piccole onde, forzandole a diventare piu' grandi. Il vento che soffia sopra le onde produce differenze di pressione lungo il profilo dell'onda, che induce l'onda a crescere. Il processo e' instabile perche', come l'onda diventa piu' grande, la differenza di pressione aumenta, e l'onda cresce piu' rapidamente. L'instabilita' induce l'onda a crescere esponenzialmente (Miles, 1957).
3. Finalmente, le onde cominciano ad interagire tra loro per produrre onde piu' lunghe (Hasselmann et al., 1973). L'interazione trasferisce energia alle onde grandi dalle onde piu' piccole generate dal meccanismo di Miles con frequenze leggermente piu' basse di quelle al picco dello spettro (Figura 16.10). Eventualmente, questo porta ad onde che vanno piu' veloci del vento, come notato da Pierson e Moskowitz.

16.5 La Previsione delle Onde

La nostra comprensione delle onde del Mare, i loro spettri, la loro generazione dal vento, e le loro interazioni sono ora sufficientemente ben conosciute che lo spettro delle onde puo' essere previsto usando i venti calcolati dai modelli numerici atmosferici. Se osserviamo alcune piccole aree dell'Oceano, o alcune aree al largo, possiamo vedere le onde generate dai venti locali, il mare vivo (wind sea), piu' le onde che sono state generate in altre aree e che si sono propagate fino alla zona che stiamo osservando, l'onda lunga (swell). La previsione delle onde locali deve includere entrambi : il mare vivo e l'onda lunga, quindi la previsione delle onde non e' un problema locale. Vediamo, per esempio, che le onde al largo della California possono essere generate da tempeste lontane piu' di 10 000 km.

Varie tecniche sono state usate per prevedere le onde. I primi tentativi erano basati su relazioni empiriche tra l'altezza e la lunghezza delle onde con la velocita' del vento, la durata, ed il 'fetch'. Lo sviluppo dello spettro delle onde permise l'evoluzione delle componenti individuali delle onde con la frequenza f che viaggiano in direzione θ, dello spettro direzionale delle onde ψ (f, θ) usando

(16.39)

dove ψ₀ = ψ₀ (f,θ ; x, t ) varia nello spazio (x) e nel tempo t, S_i e' l'input del vento dato dal meccanismo di Phillips (1957) e Miles (1957), S_nl e' il trasferimento tra componenti d'onda dovuto ad interazioni non-lineari (Figura 16.10), e S_d e' la dissipazione.

I modelli di terza generazione per la previsione delle onde, usati ora dalle agenzie meteorologiche di tutto il mondo sono basati sulla integrazione della (16.39) usando molte componenti individuali delle onde (il gruppo SWAMP, 1985; il gruppo WAMDI,1988; Komen et al., 1994). Le previsioni seguono i componenti individuali dello spettro delle onde nello spazio e nel tempo, permettendo ad ogni componente di crescere o di decadere in funzione dei venti locali e permettendo alle componenti delle onde di interagire in accordo alla teoria di Hasselmann. Tipicamente il mare e' rappresentato da 300 componenti: 25 lunghezze d'onda che vanno in 12 directions (30°). Ad ogni componente e' permesso di propagarsi da punto a punto della griglia, crescendo con il vento o decadendo nel tempo, il tutto mentre interagisce con le altre onde dello spettro. Per ridurre il tempo di calcolo, i modelli usano griglie di punti miste: La griglia ha una alta densita' di punti nelle tempeste e vicino la costa, bassa densita' di punti nelle altre regioni. Tipicamente, i punti della griglia in mare aperto sono distanti 3°.

Alcuni modelli sperimentali fanno un passo in piu' nel processo di previsione, assimilando nel modello le osservazioni degli altimetri sulla velocita' del vento e quelle degli scatterometri sull'altezza delle onde. Le previsioni delle onde usando i dati assimilati dei satelliti sono disponibili dal ECMRF (European Centre for Medium-Range Weather Forecasts). I dettagli dei modelli di terza generazione prodotti dal Wave Analysis Group (WAM) sono descritti nel libro di Komen et al., (1994).

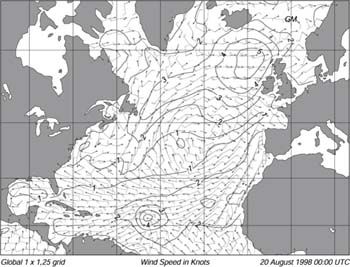
Allo Ocean Modelling Branch del NOAA, il National Centers for Environmental Predictions produce anche una previsione delle onde regionale e globale. Il Branch usa un modello di terza generazione basato sul modello Cycle-4 WAM. Tiene conto dei cambiamenti del limite dei ghiacci, e assimila i dati delle boe e degli altimetri dei satelliti. Il modello calcola gli spettri direzionali di frequenza in 12 direzioni e 25 frequenze a 3-ore di intervallo fino a 72 ore in avanti. La frequenza piu' bassa e' 0.04177 Hz e le frequenze piu' alte sono separate logaritmicamente di 0.1 volte la frequenza piu' bassa. I dati spettrali delle onde sono disponibili su una gliglia di 2.5° × 2.5° per i punti di acqua profonda tra 67.5°S e 77.5°N. Il modello e' forzato usando i venti a 10 m calcolati dai venti piu' deboli del modello atmosferico riportati all'altezza di 10 m usando un profilo logaritmico (8.19). Il Branch sta provando una previsione migliorata con una risoluzione di 1° × 1.25° (Figura 16.11).

Figura 16.10 Output del modello previsionale delle onde di terza generazione prodotta dall'Ocean Modeling Branch del NOAA per il giorno 20 Augosto 1998. I contorni sono l'altezza significativa delle onde in metri, le frecce forniscono la direzione delle onde al picco dello spettro , e le bande la velocita' del vento e la direzione. Dal Ocean Modeling Branch del NOAA.

16.6 La Misura delle Onde

Poiche' le onde influenzano tanti processi e tante operazioni a mare, molte tecniche sono state inventate per misurare le onde. Qui sono elencate alcune delle tecniche piu' usate. Stewart (1980) da' una piu' completa descrizione delle tecniche di misura delle onde, includendo i metodi per misurare la distribuzione direzionale delle onde.

Stime dello Stato del Mare da Osservatori in mare
Questa e' forse la piu' comune osservazione inclusa nelle prime tabulazioni delle altezze delle onde. Queste sono le altezze significative delle onde riassunte dalla Marina degli U.S. nei Marine Climatological Atlas ed altre pubblicazione di tale genere stampati prima dell'era dei satelliti.

Accelerometri Montati su Boe Meteorologiche o di altro Tipo
Questa e' una misura meno comune, sebbene e' usata spesso per misurare le onde durante esperimenti di breve durata. Per esempio, gli accelerometri sulle navi meteorologiche misurano l'altezza delle onde secondo Pierson & Moskowitz e le osservazioni sono mostrate nella Figura 16.2. Le misure piu' accurate sono fatte usando un accelerometro stabilizzato da un giroscopio in modo che l'asse dell'accellerometro e' sempre verticale.

La doppia integrazione dell'accelerazione verticale da' uno spostamento. La doppia integrazione,comunque, amplifica il rumore a bassa frequenza, che porta a segnali di bassa frequenza visti nelle Figure 16.4 e 16.5. Inoltre, la grossa boa non e' sensibile alle lunghezze d'onda minori del diametro, e le boe misurano solo onde che hanno lunghezze dell'onda piu' grandi del diametro della boa. Nell'insieme, le misure migliori sono accurate al ±10% o piu'.

Misuratori d'Onda
I congegni possono essere montati su piattaforme o sul fondo marino in acque poco profonde. Molti tipi differenti di sensori sono usati per misurare l'altezza delle onde oppure la pressione sub-superficiale che e' collegata all'altezza dell'onda. Il suono, i raggi infrarossi, le onde radio possono essere usati per determinare la distanza dal sensore alla superfice marina a patto che il sensore sia montato su una piattaforma stabile che non interferisce con l'onda. I misuratori di pressione descritti nel §6.8 possono essere usati per misurare la profondita' dalla superfice del mare allo strumento. Una serie di misuratori di pressione opportunamente posizionati sul fondo sono utili a determinare la direzione delle onde. Queste configurazioni sono ampiamente usate appena fuori della zona di 'surf' per determinare la direzione delle onde al largo.

I misuratori di pressione devono essere posizionati dentro la zona con profondita' di un quarto della lunghezza d'onda poiche' le fluttuazioni di pressione indotte dalle onde decrescono esponenzialmente con la profondita'. Cosi', l'uso di questi strumenti e' ristretto ad acque poco profonde o a grandi piattaforme posizionate sulla piattaforma continentale. Di nuovo, l'accuratezza e' di ±10%.

Gli Altimetri dei Satelliti
Gli altimetri dei satelliti usati per misurare le correnti geostrofiche di superfice misurano anche l'altezza delle onde. Gli altimetri hanno volato sul Seasat nel 1978, su Geosat dal1985 al1988, su ERS-1 & 2 dal 1991, sul Topex/Poseidon dal1992, e su Jason dal 2001. I dati degli altimetri sono stati usati per produrre mappe medie mensili dell'altezza delle onde e la variabilita' della densita dell'energia delle onde nel tempo e nello spazio. Il prossimo passo, appena cominciato, e' usare le osservazione altimetriche con i programmi di previsione delle onde, per aumentare l'accuratezza della previsione.

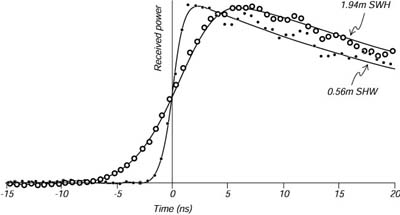
La tecnica degli altimetri lavora come segue. L'impulso radio inviato dallo strumento sul satellite e' riflesso prima dalla cresta e poi dal cavo delle onde. La riflessione allunga l'impulso dell'altimetro nel tempo, e l'allungamento e' misurato ed usato per calcolare l'altezza dell'onda (Figure 16.12). L'accuratezza e' di ±10%.

16.11 Forma dell'impulso radio ricevuto dall'altimetro del Seasat, che mostra l'influenza delle onde oceaniche. La forma dell'impulso e' usata per calcolare l'altezza significativa delle onde. Da Stewart (1985).

I Radar ad Apertura Sintetica (SAR) sui Satelliti
Questi radar mappano la riflettivita' del radar sulla superfice marina con una risoluzione spaziale di 6- 25 m. Le mappe di riflettivita' mostrano spesso caratteristiche 'quasi come onde' collegate alle onde vere della superfice marina. Diciamo ' quasi come onde' perche' non sono relazioni uno ad uno tra altezza dell'onda e densita' dell'immagine. Alcune onde sono chiaramente mappate, altre meno. Le mappe, comunque, possono essere usate per ricavare ulteriori informazioni sulle onde, specialmente la distribuzione spaziale della direzione delle onde in acque poco profonde (Vesecky e Stewart, 1982). Poiche' l'informazione sulla direzione puo' essere calcolata direttamente dai dati dei radar senza bisogno di processare un'immagine (Hasselmann, 1991), i dati dei radar e degli altimetri su ERS-1 & 2 possono essere usati direttamente nei programmi di previsione delle onde.

16.7 Concetti Importanti

1. La lunghezza e la frequenza delle onde sono collegate attraverso la relazione di dispersione.
   
   
2. La velocita' della fase dell'onda puo' differire dalla velocita' a cui l'energia dell'onda si propaga.
   
   
3. Le onde in acque profonde sono dispersive, le onde con lunghezza piu' lunga viaggiano piu' veloci di quelle con lunghezza piu' corta. Le onde in acque basse non sono dispersive.
   
   
4. La dispersione delle onde oceaniche e' stata misurata accuratamente, e le osservazioni delle onde disperse puo' essere usata per tracciare la zona di origine delle tempeste lontane.
   
   
5. La forma della superfice marina risulta dalla sovrapposizione di tutte le possible lunghezze o frequenze delle onde che viaggiano in tutte le possibili direzioni.
   
   
6. Lo spettro fornisce i contributi alla varianza degli spostamenti superficiali in funzione della frequenza o lunghezza d'onda.
   
   
7. L'energia dell'onda e' proporzionale alla varianza dello spostamento superficiale.
   
   
8. Gli spettri digitali sono a banda limitata, e non contengono informazioni sulle onde con frequenze piu' alte a quella di Nyquist.
   
   
9. Le onde sono generate dal vento. I forti venti di lunga durata generano le onde piu' grandi.
   
   
10. Varie forme idealizzate dello spettro delle onde generate da venti omogenei e stazionari sono state proposte. Le due piu' importanti sono lo spettro di Pierson-Moskowitz e quello di JONSWAP.
    
    
11. Le Osservazioni dei naviganti sulle navi e quelle degli altimetri sui satelliti sono state usate per fare mappe globali dell'altezza delle onde. Misuratori di onda sono usati sulle piattaforme in acque poco profonde e nelle piattaforme continentali. Misuratori di pressione posizionati sul fondo sono usati per osservare le onde al largo delle coste. Ed i radar ad apertura sintetica sono usati per avere informazioni sulla direzione delle onde.