Capitolo 7 - Un Po' di Matematica : Le Equazioni del Moto

In questo capitolo consideriamo la risposta di un fluido alle forze interne ed esterne. Questo porta alla derivazione di alcune equazioni di base che descrivono la dinamica dell'oceano. Nel prossimo capitolo, prenderemo in esame la viscosita' (l'attrito interno di un fluido), e nel capitolo 12 le conseguenze della vorticita'.

La Meccenica dei Fluidi usata in oceanografia e' basata sulla Meccanica Newtoniana modificata dalla nostra (evolvente) comprensione della turbolenza. La conservazione della massa, del momento, del momento angolare, e dell'energia porta a particulari equationi, che hanno nomi che nascondono le loro origini (Tabella 7.1).

7.1 Le Forze Dominanti nella Dinamica dell'Oceano

Soltanto poche forze sono importanti in Oceanografia Fisica: la gravita', la spinta idrostatica dovuta alle differenze di densita' dell'acqua marina, e lo sforzo del vento (Tabella 7.2).

Ricordiamoci che le forze sono vettori. Hanno cioe' non solo una grandezza, ma anche una direzione.

1. Gravita' e' la forza dominante. Il peso dell'acqua nell'Oceano produce pressione. I cambiamenti nella gravita', dovuti al Sole ed alla Luna in relazione alla Terra producono le maree, le correnti di marea, ed il mescolamento mareale all'interno dell'oceano.
   
   Spinta Idrostatica e' la forza verso l'alto o verso il basso, dovuta alla gravita' su una porzione di acqua che e' piu' o meno densa di quella vicina. Per esempio, aria fredda che soffia sul mare raffredda la superfice marina, facendola diventare piu' densa degli strati sottostanti. La gravita', agendo sulla differenza di densita', produce una forza che fara' affondare l'acqua piu' densa.
   
   Gradienti Orizzontali di Pressione sono dovuti al differente peso dell'acqua in regioni adiacenti dell'Oceano.
   
   
2. Attrito (friction) e' la forza che agisce su un corpo che si muove su un altro mentre sono in contatto. I corpi possono essere porzioni di acqua o di aria.
   
   
3. Pseudo-forze sono forze apparenti che vengono dal movimento curvilineo o dai sistemi di coordinate in rotazione. Percio', scrivendo le equazioni del moto inerziale in un sistema di coordinate in rotazione, ........porta a termini di forza aggiuntivi chiamati pseudo-forze. Per esempio, La prima legge di Newton stabilisce che non c'e' cambiamento del moto di un corpo se non ci sono forze che agiscono su di lui. Ancora un corpo che si muove a velocita' costante, sembra cambiare direzione quando viene visto da un sistema di coordinate rotanti. Il cambio in direzione e' attribuito alla pseudo-forza, la forza di Coriolis.
   
   Forza di Coriolis e' la pseudo-forza dominante che influenza le currenti esistenti in un sistema di coordinate solidale con la Terra.

7.2 I Sistemi di Coordinate

I sistemi di coordinate ci permettono di facilitare il lavoro nella teoria e nella pratica. I vari sistemi, dipendenti dalle dimensioni delle caratteristiche, sono usati per descivere e per mappare. Io preferisco i sistemi piu' semplici; le descrizioni degli altri sistemi possono essere trovate nei libri di geografia e di geodesia.

1. Sistema di Coordinate Cartesiane e' quello che uso comunemente nei seguenti capitoli per mantenere la discussione piu' semplice possibile. Possiamo descrivere la maggioranza dei processi in coordinate cartesiane senza la complessita' matematica delle coordinate sferiche. La convenzione in uso nella meccanica dei fluidi geofisici e' x verso est, y e' verso nord, e z e' verso l'alto.
   
   piano-f e' un sistema di coordinate cartesiane nel quale la forza di Coriolis e' assunta constante. E' utile per descrivere il flusso in regioni piccole comparete al raggio della Terra e piu' grandi di poche decine di kilometri.
   
   piano-β e' un sistema di coordinate Cartesiane in cui la forza di Coriolis e' assunta variabile linearmente con la latitudine. E' utile per descrivere il flusso su grandi aree come i bacini oceanici.
   
   
2. Coordinate Sferiche sono usate per descrivere i flussi che si estendono su grandi distanze e nei calcoli numerici dei flussi di scala globale e di bacino.

7.3 I Tipi di Flusso nell'Oceano

Molti termini sono stati usati per descrivere la circolazione degli Oceani. Di seguito sono riportati i termini piu' comunemente usati per descrivere le correnti e le onde.

1. Circolazione Generale e' la circolazione permanente e mediata nel tempo.
2. Circolazione Meridionale ??? Overturning ??? conosciuta anche come Circolazione Termoalina e' la circolazione, ??? nel piano meridionale ??? , guidata dal mescolamento.
3. Circolazione Forzata dal Vento e' la circolazione nel primo kilometro del mare forzata dal vento. La circolazione puo' essere causata da venti locali o dai venti in altre regioni.
4. Gyre sono correnti cicloniche o anti-cicloniche forzate dal vento con dimensioni vicine ai bacini oceanici.
5. Correnti di Confine (Boundary Currents) sono correnti parallele alle coste. Due tipi di correnti di confine sono importanti:
   • boundary currents occidentali, sono sui bordi occidentali degli oceani, tendono ad essere veloci e strette come la "Gulf Stream" ed il "Kuroshio".
   • "boundary currents" orientali sono deboli, e.g. la corrente della California.
6. Squirts or Jets sono correnti strette, con le dimensioni di poche centinaia di kilometri, che sono quasi perpendicolari alle coste occidentali.
7. Vortici di Mesoscala sono flussi turbulenti o ruotanti delle dimensioni di poche centinaia di kilometri.

In aggiunta ai flussi dovuto alle correnti, ci sono molti tipi di flussi oscillatori dovuti alle onde. Normalmente, quando pensiamo alle onde del mare, ci riferiamo alle onde che si rompono sulla spiaggia oppure le onde di superfice che influenzano le navi in mare. Ma molti altri tipi di onde esistono nell'Oceano.

1. Onde Planetarie dependono dalla rotazione Terrestre ...... ?? of the Earth for a restoring force ?? , ed includono onde di Rossby, di Kelvin, Equatoriali, e di Yanai.
2. Onde di Superfice talvolta dette onde di gravita' , sono le onde che vediamo rompersi sulla spiaggia. La forza e' dovuta al grande contrasto di densita' tra aria e acqua alla superfice marina.
3. Onde Interne sono onde sommerse simili a quelle di superfice. La forza ... e' dovuta alle differenze di densita' con la profondita'.
4. Tsunami sono onde di superfice molto lunghe (con periodo di 15 minuti) generate dai terremoti.
5. Correnti di Marea sono correnti orizzontali e correnti associate con onde interne forzate dalle foze di marea.
6. Onde di Bordo (Edge Waves) Sesse ? sono onde con periodo di pochi minuti in regioni a basso fondale vicino alle spiagge. L'ampiezza di queste onde scende esponenzialmente con la distanza dalla spiaggia.

7.4 La Conservazione della Massa e del Sale

La conservazione della massa e del sale puo' essere usata per ottenere informazioni molto utili sui flussi nell'oceano. Per esempio, supponiamo che vogliamo sapere la perdita netta di acqua dolce, l'evaporazione meno la precipitazione, del Mare Mediterraneo. Potremmo calcolare con molta cura il flusso di calore latente sopra la superfice, ma probabilmente ci sono troppo pochi rapporti di navi per una applicazione sensata della bulk formula. Oppure potremmo misurare con precisione la massa di acqua che fluisce dentro e fuori del Mediterraneo attraverso lo Stretto di Gibilterra; ma la differenza e' piccola e non puo' essere misurata con sufficiente accuratezza (Bryden and Kinder, 1991).

Possiamo, comunque, calcolare la evaporazione netta conoscendo la salinita' del flusso di entrata S_i e di uscita S_o, insieme ad una rozza stima del volume di acqua V_o che esce, dove V_oe' il volume del flusso in unita' di m³/s (Figura 7.1).

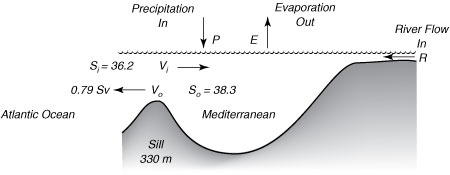Figura 7.1 Diagramma schematico del flusso che entra ed esce da un bacino. Valori da Bryden e Kinder (1991).

Il flusso di massa entrante, e' per definizione, ρ_o V_o. Se il volume del mare non cambia, la conservazione della massa richiede:

dove, ρ_i , ρ_o sono le densita' dell'acqua che entra ed esce. Di solito, possiamo assumere, con un piccolo errore, che ρ_i = ρ_o.

se c'e' precipitazione P ed evaporazione E alla superfice del bacino ed il contributo dei fiumi R, la conservazione della massa diventa:

Risolvendo per (V_o - V_i ):

che stabilisce che il flusso netto dell'acqua nel bacino deve bilanciare le precipitazioni piu' il contributo dei fiumi meno l'evaporazione quando sufficientemente mediato su un tempo lungo.

Poiche' il sale non e' depositato o rimosso dal mare, e poiche' la salinita' del Mediterraneo non e' cambiata, la conservazione del sale richiede:

dove ρ_i, S_i sono la densita' e la salinita' dell'acqua entrante, e ρ_o, S_o sono la densita e la salinita' del flusso di uscita. Con un piccolo errore, possiamo di nuovo assumere che ρ_i = ρ₀.

Un Esempio di Conservazione della Massa e del Sale
Usando i valori per il flusso dello Stretto di Gibilterra misurato da Bryden e Kinder (1991) e mostrato in figura 7.1, risolvendo (7.4) per V_i assumendo che ρ_i = ρ_o, ed usando i valori stimati di V_o da' V_i = 0.836 Sv = 0.836 × 10 ⁶ m³/s, dove Sv = Sverdrup = 10⁶ m³/s e' l'unita' di flusso usato in oceanografia. Usando V_i e V_o in (7.3) si ottiene (R + P - E) = -4.6 × 10⁴ m³/s.

Conoscendo V_i, possiamo anche calcolare il tempo minimo di residenza dal flusso entrante. Il tempo minimo di residenza T_m e' il volume del mare diviso per il volume dell'acqua entrante. Il Mediterraneo ha un volume di circa 4 × 10⁶ km³. Convertendo 0.836 × 10⁶ m³/s a km³/yr otteniamo 2.64 × 10⁴ km³/yr. Allora, T_m = (4 × 10⁶ km³)/(2.64 × 10 ⁴ km³/yr) = 151 yr. Il tempo attuale dipende dal mescolamento all'interno del mare. Se le acque sono ben mescolate, il tempo di scarica e' vicino al tempo minimo, se non sono ben mescolate, il tempo di scarica e' piu' lungo.

Il nostro esempio di flusso entrante ed uscente dal Mare Mediterraneo e' un esempio di box model. Un "box model" rimpiazza grossi sistemi, come il Mar Mediterraneo, con scatole. I fluidi o gli elementi chimici o gli organismi possono muoversi tra le scatole, e le equazioni conservative sono usate per confinare le interazioni dentro i sistemi.

7.5 La Derivata Totale (D/Dt)

Se il numero delle box in un sistema cresce fino ad un numero molto grande, la dimensione di ogni box si riduce, fino ad avvicinarci ai limiti usati nel calcolo differenziale.

Per esempio, se suddividiamo il flusso di acqua nei box a pochi metri per lato, e se usiamo la conservazione della massa e del momento, oppure altre propieta' dentro ogni box, possiamo derivare le equazioni differenziali che governano il flusso fluido.

Consideriamo il semplice esempio della accelerazione del flusso in una piccola box del fluido. La equazione risultante e' chiamata derivata totale. Relazione l'accelerazione della particella Du/Dt alle derivate del campo di velocita' al punto fisso nel fluido. Useremo l'equazione per derivare le equazioni per il moto del fluido dalla Legge di Newton che richiede di calcolare le accelerazioni di una particella passante per un punto fisso del fluido.

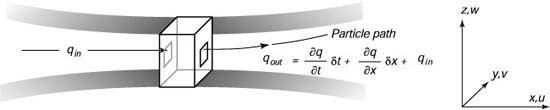Figura 7.2 Schema del flusso usato per calcolare la derivata totale.

Cominciamo dal considerare il flusso di una quantita' q_in che entra ed una q_out che esce dalla piccola box schematizzata in Figura 7.2. Se q puo' cambiare continuamente nel tempo e nello spazio, la relazione tra q_in and q_out e':

(7.5)

Il tasso di cambiamento della quantita' q dentro il volume e':

(7.6)

Ma δx/δt e' la velocita' u; quindi:

In tre dimensioni, la derivata totale diventa:

	(7.7a)
	(7.7b)

dove u e il vettore velocita' e ∇ e' l'operatore del della teoria del campo vettoriale (vedi Feynman, Leighton, e Sands 1964: 2-6).

Questo e' un risultato sorprendente. La semplice trasformazione delle coordinate, dal seguire la particella a coordinate fisse nello spazio, converte una semplice derivata lineare in una derivata parziale non-lineare. Ora usiamo l'equazione per calcolare il cambio del momento di una porzione di fluido.

7.6 L'Equazione del Momento

La Seconda Legge di Newton mette in relazione le variazioni del momento di una massa fluida con la forza applicata. Il cambio e':

(7.8)

dove F e' la forza, m la massa, e v e' la velocita'; e dove abbiamo enfatizzato il bisogno di usare la derivata totale perche' stiamo calcolando la forza applicata ad una particella.. Possiamo assumere che la massa sia costante, e la (7.8) puo' essere scritta:

(7.9)

dove f_m e' la forza per unita' di massa.

Quattro forze sono importanti: i gradienti di pressione, la forza di Coriolis, la gravita', e l'attrito. Senza derivare la forma di queste forze (le derivazioni sono date nel prossimo capitolo ?? the next section?? ), possiamo scrivere la (7.9) nella seguente forma.

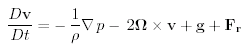(7.10)

L'accelerazione uguaglia il gradiente di pressione negativo meno la forza di Coriolis piu' la gravita' piu' le altre forze. Qui g e' l'accelerazione di gravita', F_re' l'attrito, e Ωe' la Velocita' Angolare della Terra, 2π radiante per giorno siderale o

(7.11)

Equazione del Momento in Coordinate Cartesiane:
Espandendo le derivate nella (7.10) e scrivendo le componenti in un sistema di coordinate Cartesiane si ottiene l'Equazione del Momento:

	(7.12a)
	(7.12b)
	(7.12c)

dove F_i sono le componenti di ogni forza di attrito per unita' di massa, e φ e' la latitudine. In aggiunta, abbiamo assunto che w << v, cosi' la 2 Ω w cos φ e' stata soppressa dall'equazione in (7.12a).

L'equazione (7.12) appare sotto vari nomi. Leonhard Euler (1707-1783) per primo scrisse la forma generale per un flusso fluido con le forze esterne, e talvolta la equatione e' chiamata equazione di Euler o l'equazione della accelerazione . Louis Marie Henri Navier (1785-1836) aggiunse il termine dell'attrito, e cosi' viene anche chiamata equazione di Navier-Stokes.

Il termine 2 Ω u cos φ nella (7.12c) e' piccolo comparato con g, e puo' essere ignorato nella dinamica dell'oceano. Non puo' essere ignorato, comunque, per studi sulla gravita' fatti con gravimetri sulle navi.

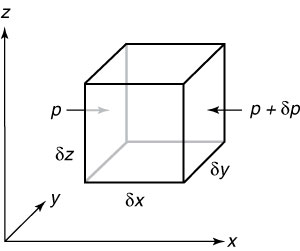Figura 7.3 Schema del flusso usato per derivare il termine della pressione nell'equazione del momento.

Derivazione del termine della Pressione
Consideriamo le forze che agiscono sui lati di un piccolo cubo di fluido (Figure 7.3). La forza netta δF_x nella direzione x e'

But

e quindi

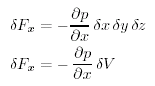Dividendo per la massa del fluido δm nel box, l'accelerazione del fluido nella direzione x e':

	(7.13)

Le forze di pressione e l'accelerazione dovuta alle forze di pressione nella direzione y e z sono derivate nello stesso modo.

Il Termine di Coriolis nell'Equazione del Momento
Il termine di Coriolis esiste perche' descriviamo le currenti in un sistema di riferimento solida con la Terra. La derivazione del termine di Coriolis non e' semplice. Henry Stommel, il noto oceanografo del Woods Hole Oceanographic Institution scrisse un libro sull'argomento insieme a Dennis Moore (Stommel & Moore, 1989).

Di solito, stabiliamo che la forza per unita' di massa, l'accelerazione di una porzione di fluido in un sistema rotante, puo' essere scritto:

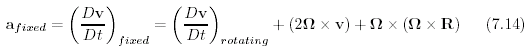(7.14)

dove R e' il vettore distanza dal centro della Terra, Ω e' il vettore della velocita' angolare della Terra, e v e' la velocita' di una porzione di fluido in coordinate fisse alla Terra. Il termine 2Ω × v e' la forza di Coriolis, ed il termine Ω × Ω × R) e' la accelerazione centrifuga. L'ultimo termine e' incluso nella gravita' (Figure 7.4).

Il Termine della Gravita' nell'Equazione del Momento L'attrazione gravitazionale di due masse M₁ and m e':

dove R e' la distanza tra le masse, e G e' la costante gravitationale. Il vettore forza F_g giace lungo la linea che connette le due masse.

La forza per unita' di massa dovuta alla gravita' e':

(7.15)

dove M_Ee' la massa della Terra. Aggiungendo l'accelerazione centrifuga alla (7.15) abbiamo la gravita' g (Figura 7.4):

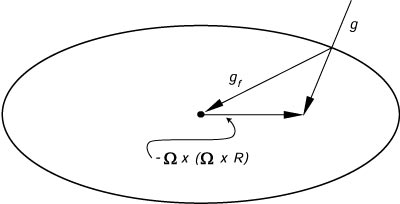Figura 7.4 L'acceleraztione verso il basso g di un corpo a riposo sulla superfice della Terra e' la somma delle accelerazioni gravitazionali tra il corpo e la massa della Terra gf e l'accelerazione centrifuga dovuta alla rotazione della Terra. Ω x (Ω x R). La superfice di un oceano a riposo deve essere perpendicolare a g, e tale superfice e' vicina ad un ellissoide di rotazione. Qui l'elletticita' terrestre e' fortemente esagerata.

Notare che la gravita' non punta verso il centro di massa della Terra. L'accelerazione centrifuga causa al filo a piombo di formare un piccolo angolo con la linea diretta al centro di massa della Terra. Come risultato, la superfice della Terra includendo la superfice dell'Oceano non e' sferica, ma e' un ellissoide allungato. Un pianeta fluido rotante ha un ingrossamento equatoriale.

7.7 La Conservazione della Massa: l'Equazione di Continuita'

Ora deriviamo l'equazione della conservazione della massa in un fluido. Cominciamo con scrivere il flusso di massa che entra e che esce da una piccola scatola (Figura 7.5).

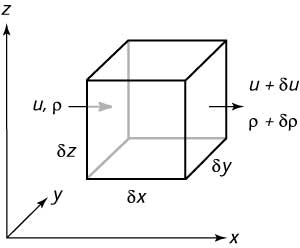Figura 7.5 Schema del flusso usato per derivare l'equazione di continuita'.

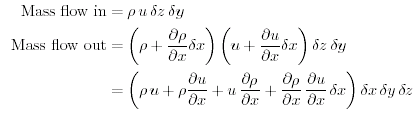Il flusso di massa nel volume deve essere ( flusso di massa uscito) - (flusso di massa entrato)

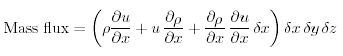Il terzo termine dentro le parentesi diventa molto piu' piccolo dei primi due quando d x si avvicina a 0; e

In tre dimensioni:

Il flusso di massa deve essere bilanciato daun cambio di massa dentro il volume, che e':

e la conservazione della massa richiede:

(7.17)

Questa e' l' equazione di continuity per un flusso compressibile, derivata per primo da Leonhard Euler (1707-1783).

L'equazione puo' essere messa in una forma alternativa espandendo le derivate dei prodotti e riarrangiando i termini per ottenere:

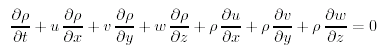I primi quattro termini costituiscono la derivata totale della densita' Dρ/Dt da (7.7), e possiamo scrivere la (7.17) come:

(7.18)

Questa e' la forma alternata dell'equazione di continuita' per un fluido compressibile.

L'Approssimazione di Boussinesq
La densita' e' quasi costante nell'Oceano, e Joseph Boussinesq (1842-1929) noto' che possiamo assumere senza rischi la densita' sia constante eccetto quando e' moltiplicata per g nei calcoli di pressione dell'Oceano. L'assunzione semplifica fortemente le equazioni del moto.

L'assunzione di Boussinesq richiede che:

1. Le velocita' nell'Oceano devono essere piccole comparete alla velocita' del suono c. Questo assicura che la velocita' non cambia la densita'. Quando la velocita' si avvicina alla velocita' del suono, i campi di velocita' possono produrre cambiamenti di densita' come le onde d'urto.
2. La velocita' di fase delle onde o dei disturbi devono essere piccoli comparati con c. La velocita' del suono in un fluido incompressibile e' infinita, e dobbiamo assumere che il fluido sia compressibile quando discutiamo del suono nell'Oceano. Percio' l'approssimazione non e' vera per il suono. Tutte le altre onde nell'Oceano hanno velocita' piccole comparate a quella del suono.
3. La scala verticale del moto deve essere piccola comparata a c²/g, dove g e' la gravita'. Questo assicura che come la pressiona aumenta con la profondita', l'aumento di pressione produce soltanto piccoli cambiamenti di densita'.

Le approssimazion(i ??) sono vere per i flussi oceanici, e assicurano che i flussi dell'Oceano sono non-compressibili. Per una descrizione piu' completa dell'approssimazione, vedi Kundu (1990: 79 e 112), Gill (1982: 85), Batchelor (1967: 167), o altri testi sulla dinamica dei fluidi.

Compressibilita'
l'assunzione di Boussinesq e' equivalente ad assumere che lacqua di mare sia incompressibile. Ora vediamo come l'assunzione semplifica l'equazione di continuita'. Definiamo il coefficiente di compressibilita'

dove V e' il volume, e p e' la pressione. Per flussi incompressibili, β = 0, e:

poiche' dp/dt Non e' uguale a 0. Ricordiamo che la densita' e' la massa m per unita' di volume V, e che la massa e' constante:

Se il flusso e' non-compressibile, la (7.18) diventa:

(7.19)

Questa e' la Equazione di Continuita' per Flussi Incompressibili.

7.8 Le Soluzioni alle Equazioni del Moto

Le equazioni (7.12) e (7.19) sono quattro equazioni, le componenti dell' equazione del momento piu' l'equazione di continuita', con quattro incognite: u, v, w, p. In linea di principio, con le appropiate condizioni al contorno, dovremmo essere in grado di risolvere le equazioni

Da Notare, comunque, che queste sono equazioni non-lineari a derivata parziale. La conservazione del momento, quando e' applicata ad un fluido, converte una semplice equazione differenziale ordinaria di primo ordine per la velocita' (Seconda Legge di Newton) , che e' di solito facile da risolvere, in una equazione alle derivate parziali non-lineare, che e' impossibile da risolvere.

Condizioni al Contorno (Boundary Conditions):
In meccanica dei fluidi, generalmente si assume:

1. Non ci sono velocita' perpendicolari al contorno, vuol dire che non ci sono flussi attraverso i bordi; e
2. Non ci sono flussi paralleli ai bordi solidi, vuol dire che non c'e' ??? slip ??? ai contorni solidi.

Soluzioni
Ci si aspetta che quattro equazioni in quattro incognit, piu' le condizioni al contorno, diano un sistema di equazioni che in teoria puo' essere risolto. In pratica, le soluzioni sono difficili da trovare anche per il piu' semplice dei flussi. Primo, per quello che so', non ci sono soluzioni esatte per le equazioni con l'attrito. Ci sono pochissime soluzioni esatte per le equazioni senza l'attrito. Per quelli interessati alle onde dell'Oceano, possono notare che una di tali soluzioni esatte e' quella di Gerstner per le onde di acqua (Lamb, 1945: 251). Poiche' le equazioni sono impossibili da risolvere, cercheremo i modi per semplificare fortemente le equazioni. Piu' avanti troveremo che anche i calcoli numerici sono difficili.

Le soluzioni analitiche possono essere ottenute per forme delle equazioni del moto, molto semplificate. Tali soluzioni sono usate per studiare i processi dell'oceano, che includono le onde. Le soluzioni per i flussi oceanici con coste realistiche e le caratteristiche del fondo, devono essere ottenute da soluzioni numeriche. Nei prossimi capitoli vedremo le soluzioni per le forme semplificate delle equazioni. Nel Capitolo 15 considereremo le soluzioni numeriche.

7.9 Concetti Importanti

1. La gravita', la spinta idrostatica, ed il vento sono le forze dominanti che agiscono sull'Oceano.
   
   
2. La rotazione della Terra produce una pseudo forza, la forza di Coriolis.
   
   
3. Le leggi di conservazione applicate al flusso nell'Oceano portano alle equazioni del moto; la conservazione del sale, del volume e delle altre quantita' possono portare a considerazioni profonde sul flusso oceanico.
   
   
4. La transformazione, dalle equazioni del moto applicate a porzioni fluide a quelle applicate adun punto fisso nello spazio, complica considerevolmente le equazioni del moto. Le equazioni differenziali ordinarie, lineari di primo grado, che descivono la dinamica Newtoniana di una massa di acqua accellerata da una forza, diventano equazioni della meccanica dei fluidi non lineari, a derivate parziali.
   
   
5. Il flusso nell'Oceano puo' essere assunto essere imcompressibile eccetto quando entra in gioco il suono. La densita' puo' essere assunta essere costante eccetto quando la densita' e' moltiplicata per la gravita' g. Questa assunzione e' chiamata approssimazione di Boussinesq.
   
   
6. La conservazione della massa porta all'equazione di continuita', che ha una forma particolarmente semplice per un fluido non-compressibile.